高等数学竞赛题解：利用求导法则解题

例2.9（浙江省2003年竞赛题）　求.

解析　应用二项式定理，有

两边求导得

两边乘以x后再求导得

令x＝1得

化简得，于是

例2.10（江苏省1998年竞赛题）　函数f（x）＝（x2＋3x＋2）｜x3－x｜的不可导点的个数为________.

解析　令u（x）＝x2＋3x＋2，v（x）＝｜x3－x｜，则u（x）处处可导，而v（x）在x＝－1，0，1处不可导，在其他点处处可导.u（－1）＝0，u（0）＝2，u（1）＝6.因f（x）＝u（x）v（x），又因为，则

令x＝－1，0，1分别代入上式得

所以f（x）在x＝－1处可导，f′（－1）＝0.f（x）在x＝0和x＝1处左、右导数不相等，所以f（x）在x＝0与x＝1处不可导，其他点处处可导.于是f（x）有2个不可导点.

例2.11（南京大学1996年竞赛题）　证明：两条心脏线ρ＝a（1＋cosθ）与ρ＝a（1－cosθ）在交点处的切线互相垂直.(www.xing528.com)

解析　曲线ρ＝a（1＋cosθ）化为参数方程为

x＝a（1＋cosθ）cosθ，　y＝a（1＋cosθ）sinθ

其斜率为

曲线ρ＝a（1－cosθ）化为参数方程为

x＝a（1－cosθ）cosθ，　y＝a（1－cosθ）sinθ

其斜率为

再求两曲线的交点.由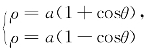解得cosθ＝0，于是交点的极坐标为.

在，因为k1k2＝－1，所以两曲线在交点处的切线互相垂直.

在，因为k1k2＝－1，所以两曲线在交点处的切线互相垂直.