高等数学竞赛题解析教程：利用导数定义解题

例2.1（北京市1994年竞赛题）　设函数f（x）在（－∞，＋∞）内有定义，对任意x都有f（x＋1）＝2f（x），且当0≤x≤1时f（x）＝x（1－x2），试判断在x＝0处函数f（x）是否可导.

解析　当－1≤x＜0时有0≤x＋1＜1，故

由于f′－（0）≠f′＋（0），故f（x）在x＝0处不可导.

例2.2（江苏省2000年竞赛题）　设f（x）可导，F（x）＝f（x）（1＋｜sinx｜），欲使F（x）在x＝0可导，则必有（　）

A.f′（0）＝0

B.f（0）＝0

C.f（0）＋f′（0）＝0

D.f（0）－f′（0）＝0

解析　由导数的定义，有

因为，所以要使上式右端极限存在，必须f（0）＝0.故选B.

例2.3（江苏省1996年竞赛题）　设当x＝0时，f′（0）≠0，则f（0）＝________.

解析　因为f（x）在x＝0处可导，所以f（x）在x＝0处连续.应用导数的定义得

由题意得f′（0）＝2f（0）·f′（0），因为f′（0）≠0，所以.

例2.4（江苏省2017年竞赛题）　已知函数y＝f（x）在x＝2处连续，且

试证f（x）在x＝2处可导，并求f′（2）.

解析　由y＝f（x）在x＝2处连续与已知极限得

因为

所以f（x）在x＝2处可导，且f′（2）＝5.

例2.5（精选题）　设，求f（x），并讨论f（x）的连续性与可导性.

解析　根据题意，有，且当x＞1时f（x）＝x2，当x＜1时f（x）＝ax＋b.则当x≠1时，f（1－）＝a＋b，f（1＋）＝1.故当＋a＋b）＝1，即a＋b＝1时f在x＝1时连续，且f（1）＝1.

又

于是仅当a＝2，b＝－1时，f在x＝1处可导.

例2.6（江苏省2006年竞赛题）　设

试问a，b，c为何值时，f（x）在x＝0处一阶导数连续，但二阶导数不存在？

解析　因f（0－）＝c，f（0＋）＝0，f（0）＝c，又f（x）在x＝0连续，所以c＝0.由

所以b＝1，且(www.xing528.com)

因f′（0－）＝1，f′（0＋）＝1，f′（0）＝1，故b＝1，c＝0时f′（x）在x＝0处连续.

又

则当2a≠－1，即时f（x）在x＝0处二阶不可导.

综上，，b＝1，c＝0为所求之值.

例2.7（江苏省1994年竞赛题）　已知f（0）＝0，f′（0）存在，求

解析　因f（0）＝0，f′（0）存在，所以

这里k＝1，2，…，n.于是n→∞时

例2.8（江苏省2016年竞赛题）　设命题：若函数f（x）在x＝0处连续，且

则f（x）在x＝0处可导，且f′（0）＝a.

判断该命题是否成立.若成立，给出证明；若不成立，举一反例并作出说明.

解析　方法1　命题成立.因为，所以

f（2x）＝f（x）＋ax＋o（x）　（x→0）

此式等价于

由此可得

由于，且f（x）在x＝0处连续，则在上式中令n→∞，可得

f（x）＝f（0）＋ax＋o（x）　（x→0）

应用可微的定义得f（x）在x＝0处可导，且f′（0）＝a.

方法2　命题成立.因为，所以

f（2x）－f（x）＝ax＋xα（x）　（x→0时α（x）→0）

由此可得

将上述n个式子相加，得

其中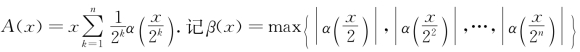，则x→0时β（x）→0，又因为，所以｜A（x）｜≤｜x｜β（x），因此A（x）＝o（x），于是有

又由于，且f（x）在x＝0处连续，在上式中令n→∞，可得

f（x）－f（0）＝ax＋o（x）　（x→0）

应用微分的定义得f（x）在x＝0处可导，且f′（0）＝a.