高等数学竞赛题解析：四则运算求极限

例1.4（江苏省2008年竞赛题）　当a＝________，b＝________时，有

解析　因为

所以a＋2＝1－b；又因为

所以a－2＝b＋1.

由上，解得a＝1，b＝－2.

例1.5（莫斯科经济统计学院1977年竞赛题）　设0，求λ，μ.

解析　由，可得

例1.6（精选题）　设f（x）是x的三次多项式，且

求.

解析　设f（x）＝A（x－2a）（x－3a）（x－4a），则

由此可得

例1.7（江苏省2012年竞赛题）　求.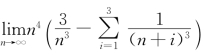

解析

例1.8（江苏省2012年竞赛题）　求.

解析　令，则

由于，故

例1.9（莫斯科公路学院1976年竞赛题）　求

解析　由于

所以

即原式＝.

例1.10（浙江省2002年竞赛题）　设.

解析应用反正切函数的和角公式，有

所以，则

例1.11（莫斯科电子技术学院1975年竞赛题）　求

解析

例1.12（莫斯科民族友谊大学1977年竞赛题）　求.

解析　由于

k3＋6k2＋11k＋5＝（k＋1）（k＋2）（k＋3）－1

所以

即原式＝.(www.xing528.com)

例1.13（江苏省2014年竞赛题）　设对每一个都是无穷小数列，其中j＝1，2，3，….现定义，若｛zk｝是一个数列，则是否一定成立？若一定成立，给出证明；若不一定成立，举一反例.

解析　不一定成立.反例如下：

当j＝1时，设

当j≥2时，设

即

则.

例1.14（浙江省2003年竞赛题）　如图所示，从正方形四个顶点P1（0，1），P2（1，1），P3（1，0），P4（0，0）开始构造P5，P6，…，使得P5为P1P2的中点，P6为P2P3的中点，P7为P3P4的中点.以此类推，我们便得到点｛Pn｝收敛于正方形内部一点P0，试求P0的坐标.

解析　设点Pn的坐标为Pn（xn，yn），则

2xn＝xn－4＋xn－3

2xn＋1＝xn－3＋xn－2

2xn＋2＝xn－2＋xn－1

2xn＋3＝xn－1＋xn

四式相加得

令n→∞，得.同理可得，即P0的坐标为.

注：若题中未说｛Pn｝收敛于P0，则还需证明｛Pn｝的收敛性.

例1.15（江苏省1991年竞赛题）　已知一点先向正东移动am，然后左拐弯移动aqm（其中0＜q＜1），如此不断重复左拐弯，使得后一段移动距离为前一段的q倍，这样该点有一极限位置，试问该极限位置与原出发点相距多少米？

解析　设出发点为坐标原点O（0，0），移动n次到达点（xn，yn）.根据移动规则，得x1＝a，x2＝a，x3＝a－aq2，x4＝a－aq2，x5＝a－aq2＋aq4，x6＝x5，x7＝a－aq2＋aq4－aq6，x8＝x7，…，归纳得

x2n－1＝a－aq2＋aq4－…＋（－1）n－1aq2（n－1），　x2n＝x2n－1

于是

同样，根据移动规则得y1＝0，y2＝aq，y3＝y2，y4＝aq－aq3，y5＝y4，y6＝aq－aq3＋aq5，y7＝y6，…，归纳得

y2n＝aq－aq3＋…＋（－1）n－1aq2n－1，　y2n＋1＝y2n

于是

故极限位置为，它与原点的距离为

例1.16（上海交通大学1991年竞赛题）　设x1＝1，x2＝2，且

求.

解析　令yn＝lnxn，则由得

故

移项得

故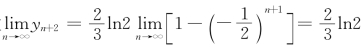，于是