和线性分析相比,非线性分析的计算时间和计算机存储量要大得多;另外,两者在数值计算方法和求解参数的设定上也有很大区别。了解非线性分析参数的含义有助于软件具体操作,主要参数归纳如下。
(1)载荷增量
对有限元求解的非线性问题,必须采用一系列带校正的线性近似来求解,即将载荷细分成一系列载荷增量,用户可以在每个载荷步内施加载荷增量,在每个增量求解完成后,继续下一个载荷增量之前,计算程序自动调整刚度矩阵以便反映结构刚度的非线性变化。矩阵刚度更新的方式包括自动更新、半自动更新和迭代控制方式,更新前的迭代次数也可以修改。
(2)载荷增量大小的选择
在非线性分析的加载过程中,选择合理的载荷增量步大小对完成分析并达到精度要求是非常重要的。较大的步长会使一个增量步中的循环计算次数增多,如果步长过大,还会导致结果精度下降甚至不收敛;而过小的步长会降低计算的效率。在软件操作过程中建议首次计算采用默认值,如果计算不收敛,则调整相关参数。
(3)收敛准则和收敛误差
在迭代过程中要设置收敛的误差值,当迭代误差小于用户设置的值时,则终止迭代。在设置误差之前,用户必须要确定收敛误差是建立在位移、载荷、功(工作)还是三者之中的任意组合的基础上。图11-2为【非线性参数】对话框中关于【收敛准则】的默认设置,其中误差的默认值为【0.01】。
(4)弧长法
求解包含各种非线性问题的常用方法,是逐个加载增量步来求解非线性力平衡方程,即在每个增量步内按给定的载荷增量或给定的位移增量,迭代出系统的平衡位置,从而追踪出结构真实的加载路径。
在增量加载分析中,包括按载荷控制的加载方式和按位移控制的加载方式,有时可以相互替代,比如对结构进行极限载荷分析时,由于极限载荷是未知的,采用载荷控制的加载方式按照事先规定的载荷增量步长加载时,一旦所施加载荷大于结构的极限载荷,就会使刚度矩阵奇异,导致求解失败。只能使用更小的载荷增量逐渐逼近极限载荷,才能获得极限载荷的近似值,但是这样操作需要反复多次才能试凑合理的加载步长,因此对于极限载荷分析问题,采用位移控制的加载方式分析更为有效。(https://www.xing528.com)
实际中往往会有更加复杂的情形,由于实际结构可能会屈曲失稳,并且所能承受的载荷极限可能有多个,都是未知的,因此试图预先给定使结构保持稳定的最大载荷和位移值,然后按照载荷控制加载或者按照位移控制加载的分析方法往往是不现实的。
近年来发展而成的弧长法控制策略则提供了解决此类问题的有效方案,其基本思想是在由弧长控制的、包含真实平衡路径的增量位移空间中,通过制定合理的约束类型,由New-ton-Raphson(牛顿-拉普森)迭代转换方法搜索满足力平衡方程的平衡路径,从而控制弧长渐进增长和方程的最终收敛。图11-3中的对话框为非线性分析类型【NLSTATIC 106】中的弧长法主要默认参数。
提示
NX Nastran结构非线性分析提供了表11-1所示的解算类型,但是在计算具体工程项目时,在操作过程中针对不同的类型,其参数的设置有所区别。
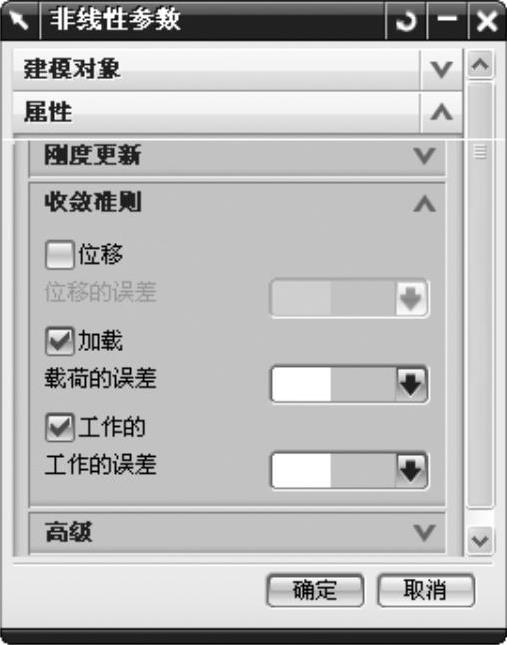
图11-2 收敛准则设置
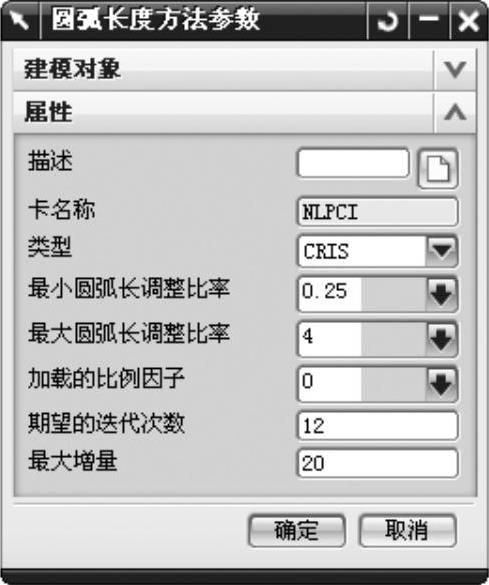
图11-3 弧长法的主要参数
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




