UGNX8.5有限元分析入门与实例：建立二力杆FEM模型

（1）建立二力杆的FEM模型

1）准备几何模型。

在三维建模环境中打开文件Book_CD\Part\Part_CAE_Unfinish\Ch07_Bar\Bar.prt，调出二力杆三维实体模型，如图7-3所示。

2）新建有限元模型。

依次单击【开始】和【高级仿真】按钮，在【仿真导航器】窗口的分级树中右键单击【Bar.prt】节点，从弹出的快捷菜单中选择【新建FEM】命令，弹出【新建部件文件】对话框。将【新文件名】下面的【名称】选项中的【fem1.fem】修改为【Bar_fem1.fem】，通过单击按钮选择本实例高级仿真相关数据存放的【文件夹】，单击【确定】按钮。

3）确定分析类型。

弹出【新建FEM】对话框，【求解器】和【分析类型】中的选项保留默认设置，如图7-4所示，单击【确定】按钮，进入创建有限元模型的环境。

4）指派材料。

单击工具栏中的【指派材料】按钮，弹出【指派材料】对话框，选中二力杆模型作为【选择体】对象，单击【材料】列表框中的【Steel】，如图7-5所示，单击【确定】按钮。

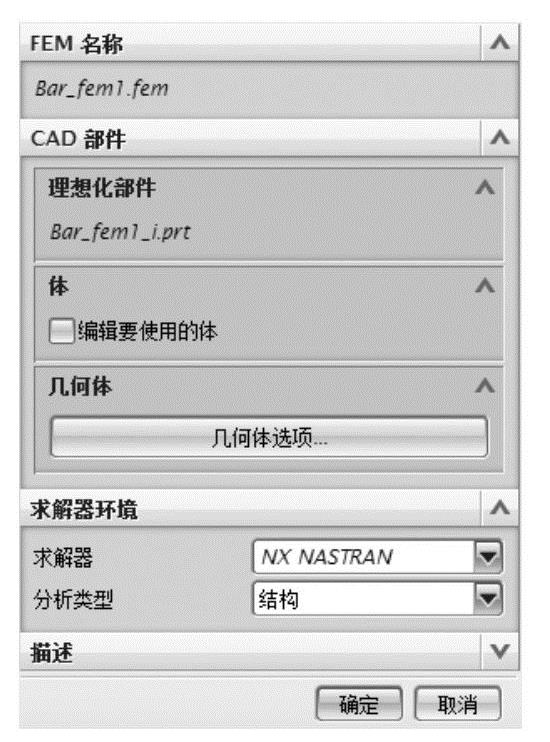
图7-4 新建二力杆FEM模型

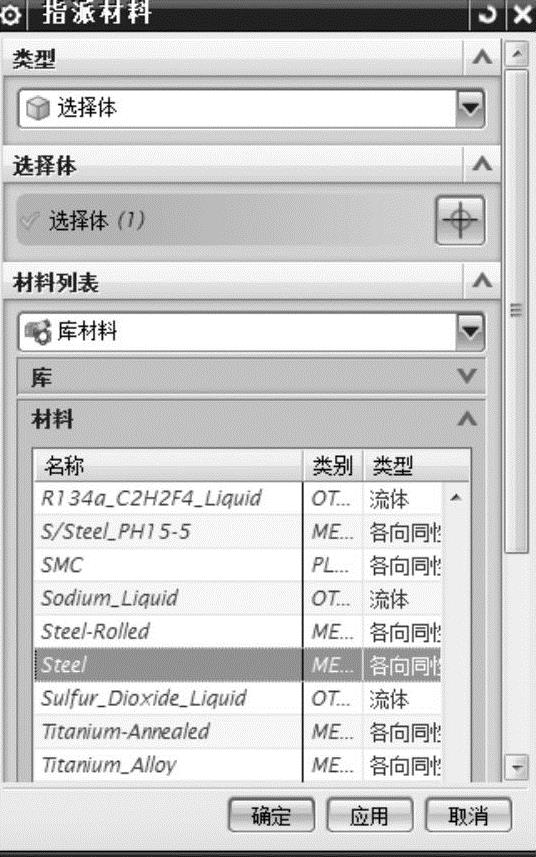
图7-5 二力杆仿真模型指派材料

5）新建物理属性。

单击工具栏中的【物理属性】按钮，弹出【物理属性表管理器】对话框，【创建】子选项【类型】默认为【PSOLID】，【名称】默认为【PSOLID1】，【标签】默认为【1】，单击【创建】按钮，弹出【PSOLID】对话框。在【材料】下拉列表框中选取【Steel】子项，其他参数均为默认值，单击【确定】按钮，如图7-6所示。

6）新建网格收集器。

单击工具栏中的【网格收集器】按钮，弹出【网格收集器】对话框。【单元拓扑结构】的各个选项保留默认设置，【物理属性】下的类型默认为【PSOLID】，在【实体类型】列表框中选取上述设置的【PSOLID1】，网格名称默认为【Solid（1）】，如图7-7所示，单击【确定】按钮。

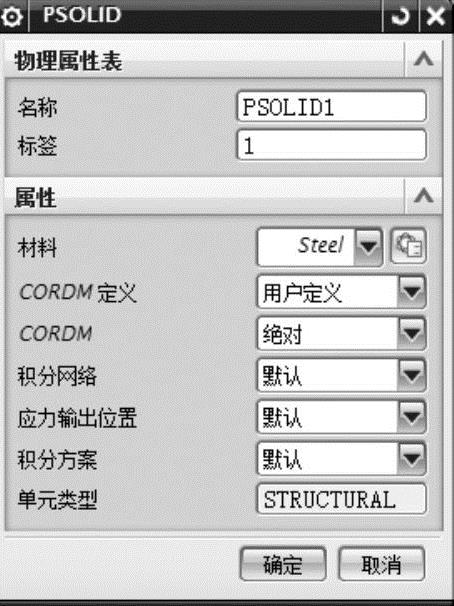
图7-6 【PSOLID】对话框

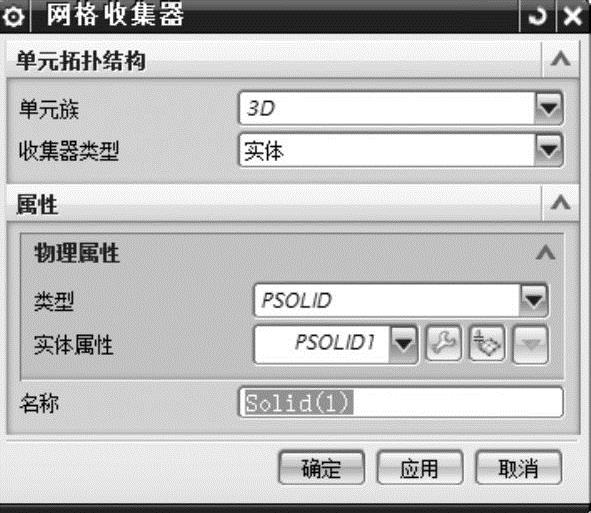
图7-7 【网格收集器】对话框

7）模型中几何体简化处理。

首先用【合并面】功能将二力杆几何模型共有多边形的几何面沿共有边进行合并，有利于后面的【拆分面】及网格划分。单击窗口上的【模型清理下拉菜单】按钮，弹出图7-8所示的下拉菜单，选择【合并面】命令，弹出【面合并】对话框，如图7-9所示。选择图7-10、图7-11中内圆和外圆的表面分界线段，发现图中的线段将消失，最后单击【确定】按钮。图7-12为完成面合并的效果。

图7-8 模型清理下拉菜单

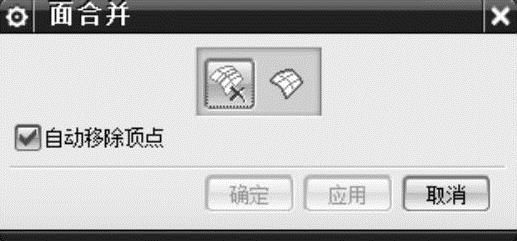
图7-9 【面合并】对话框

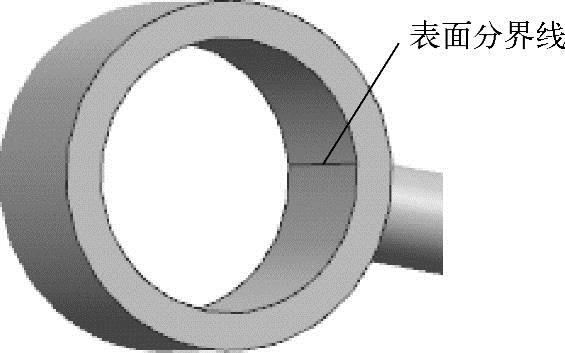
图7-10 要合并的内圆面

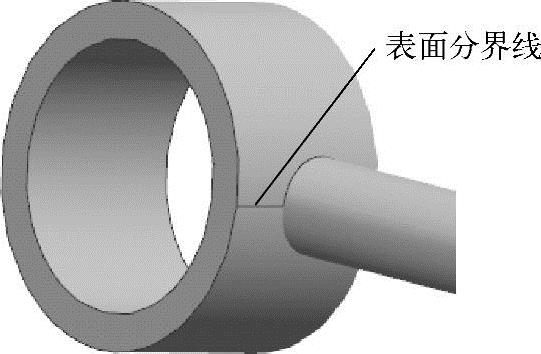
图7-11 要合并的外圆面

图7-12 合并后的效果图

8）有限元模型几何体处理———拆分面。

考虑到二力杆模型载荷与约束都是施加在半圆处，为方便在半圆处建立刚性连接，将销轴连接的内圆面分割成半圆面，后面划分的网格在此基础上建立。

a）在图7-8所示的下拉菜单中选择【拆分面】命令，弹出【拆分面】对话框，如图7-13所示，【类型】选择【通过点来分割面】，【在边上选择起始位置】中选择内圆边的1/4象限点（俗称四分点），【在边上选择结束位置】选择对面端面内圆边对应的1/4象限点，如图7-14所示，单击【应用】按钮。

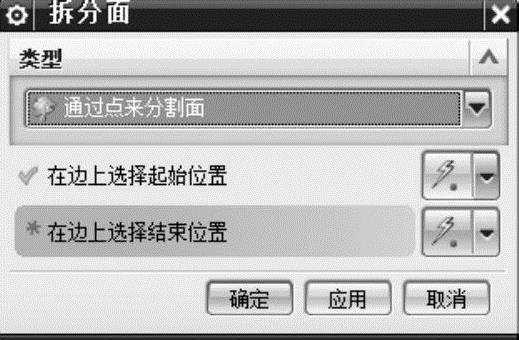
图7-13 【拆分面】对话框

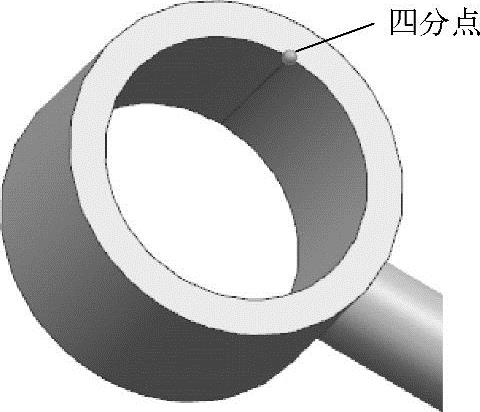
图7-14 建立拆分内圆面线段-1

b）按照上述方法，建立图7-15所示的同一内圆面对应的分割线，单击【应用】按钮。

c）同理，完成二力杆另外一侧连接内孔面的分割。可以右击分割好的半圆面，从弹出的菜单中选择【编辑显示】命令，在【常规】的【颜色】里可以选择将分割后的半圆面定义为其他颜色显示，如图7-16所示，以区别要建立刚性连接的区域。

图7-15 建立拆分内圆面线段-2

图7-16 拆分好的内圆面效果图

提示

在选择内圆边的1/4象限点时，可以将窗口中【启用捕捉点】上四分点选择功能激活，其他的点类型处于不激活状态，这样比较方便选择内圆边的1/4象限点。

9）插入刚性连接点。

在主菜单中单击【插入】按钮，在下拉菜单中依次选择【模型准备】→【点】命令，弹出【点】对话框，如图7-17所示，【类型】默认为【自动判断的点】，在【点位置】上选择二力杆一端圆孔的圆孔边在图形窗口工具栏中的【启用捕捉点】过滤中选中，然后选中二力杆一端的圆心点，此时出现图7-17所示的点输注的【X】、【Y】、【Z】轴的坐标值，将【Y】轴坐标值修改为【-1.5】，其他选项保留系统默认的参数，单击【应用】按钮；在【点位置】上选中二力杆另一端圆孔的圆孔边，在【启用捕捉点】过滤类型中选中，出现如图7-18所示的【点】对话框，输入【X】、【Y】、【Z】轴的坐标值，将【Y】轴坐标值修改为【1.5】，其他选项保留系统默认的参数，单击【确定】按钮，插入点的效果如图7-19所示。

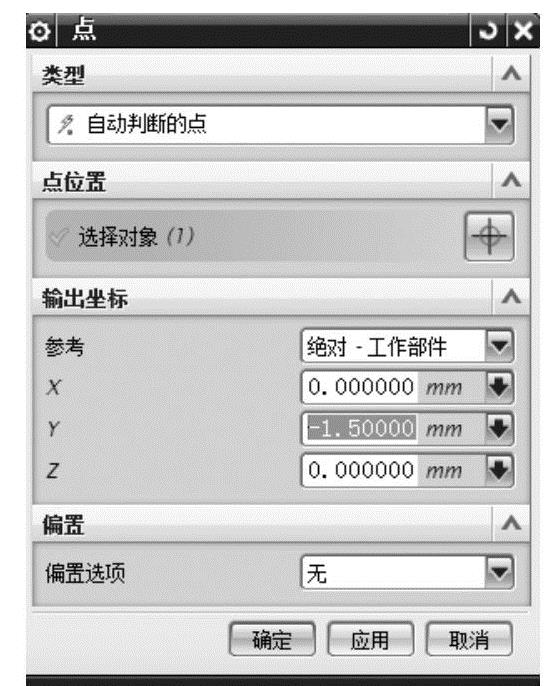
图7-17 插入一端圆孔的连接点

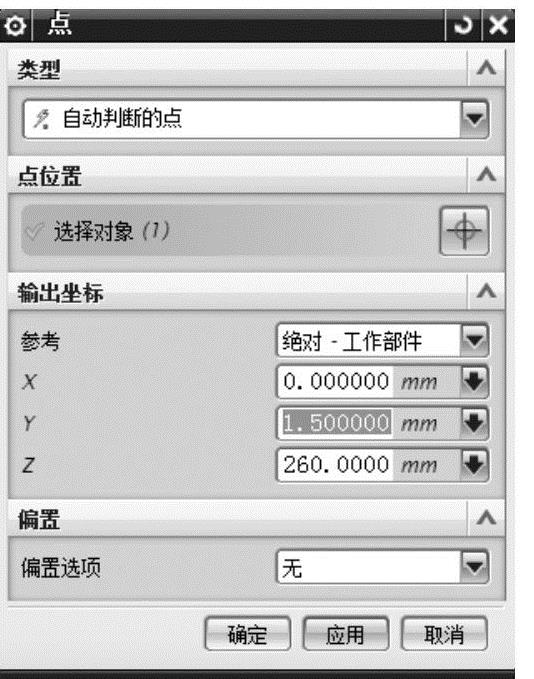
图7-18 插入另一端圆孔的连接点

图7-19 插入刚性连接点的效果图

10）网格划分。

单击工具栏中的【3D四面体网格】按钮，弹出【3D四面体网格】对话框，如图7-20所示。在图形窗口中单击二力杆模型，【类型】默认为【CTETRA（10）】，单击【单元大小】右侧的【自动单元大小】按钮，自动划分【单元大小】为【6.68】，将其修改为【3】，【单位】默认为【mm】，取消勾选【目标收集器】下面的【自动创建】复选框，将【网格收集器】右侧的选项切换为上述操作定义的【Solid（1）】，其他参数保留默认设置，单击【确定】按钮，完成二力杆模型的网格划分和参数设置操作。划分模型效果如图7-21所示。

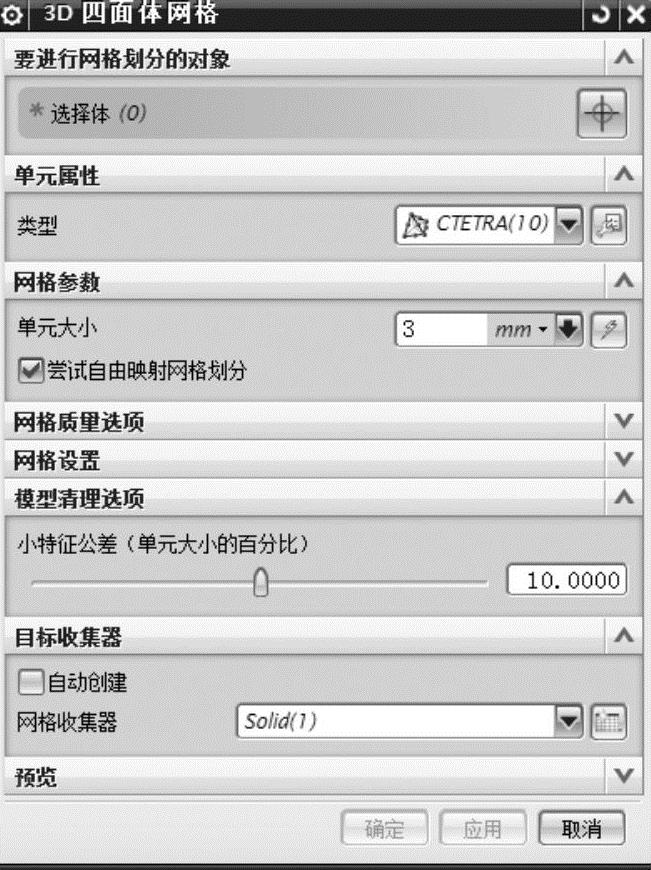
图7-20 【3D四面体网格】对话框

图7-21 二力杆FEM模型效果图

11）建立1D刚性连接。

在工具栏中单击【1D连接】按钮，出现图7-22所示的对话框。在【类型】中选中【点到面】，在【源】中选中视图窗口中二力杆一侧圆孔插入的连接点，在【目标】中选中与连接点对应的半圆内表面，在【连接单元】的【单元属性】中选择【RBE2】类型，在【目标收集器】中勾选【自动创建】复选框，如图7-22所示，单击【应用】按钮，所建立的刚性连接效果如图7-23所示。按照上面所述的方法，建立二力杆另一端圆孔半圆内表面的1D连接，最终模型的效果如图7-24所示。

至此，有限元模型准备完毕，可以进入仿真分析环境，建立包含边界约束和施加载荷条件的仿真模型了。

提示

本例中使用R型单元，R型单元是一个在节点或者与节点相连接标量点的运动分量之间施加固定约束的单元，在数学中相当于一个或几个多点约束方程（MPC）。每个约束方程都可将相关的一个自由度表示为独立自由度的线性函数。RBE2和RBE3单元是NX Nastran单元库中最常用的R型单元，其中RBE2是最常使用的刚性R型单元。在非线性屈曲分析中使用刚性的RBE2单元时要格外小心，因为没有计算较大位移的影响导致屈曲分析的结果不正确。本例中使用RBE2进行线性屈曲分析，模拟合成载荷的计算与约束的施加。

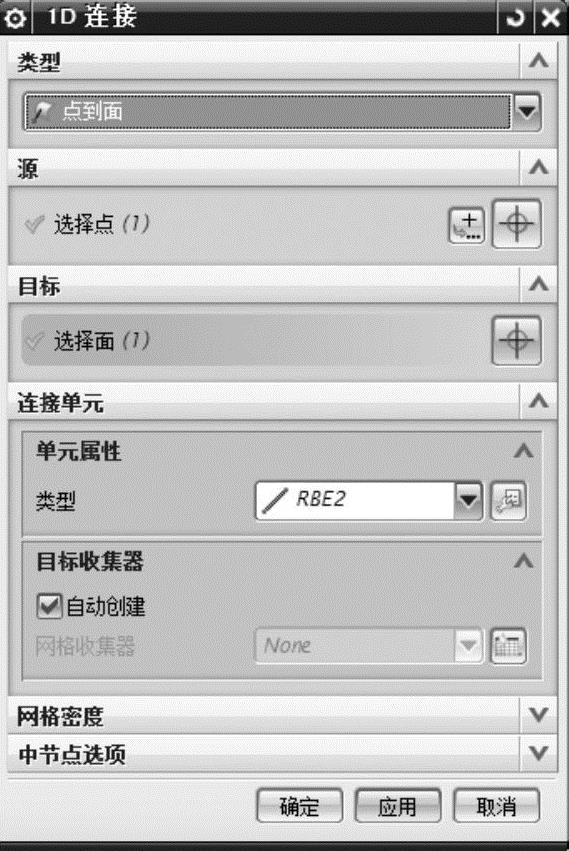
图7-22 【1D连接】对话框

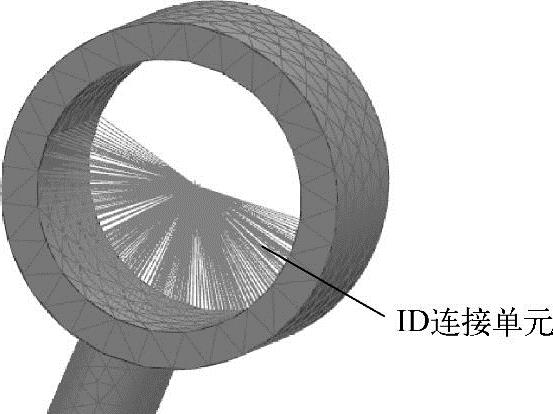
图7-23 二力杆一端圆孔1D连接效果图

图7-24 二力杆两端圆孔1D连接的效果图

（2）建立二力杆仿真模型(www.xing528.com)

1）新建仿真文件。

在【仿真导航器】窗口分级树中右击【Bar_fem1.fem】节点，从弹出的快捷菜单中选择【新建仿真】命令，弹出【新建仿真】对话框，将【新文件名】的【名称】中修改为【Bar_sim1.sim】，将文件保存到相关文件夹中，单击【确定】按钮。

2）新建线性屈曲解算方案。

弹出【新建仿真】对话框，各选项保留默认设置，单击【确定】按钮。弹出【解算方案】对话框，在【解算方案类型】下拉列表框中选择【SOL 105 Linear Buckling】解算类型，如图7-25所示，预览参数保留默认设置，单击【确定】按钮。在【仿真导航器】窗口的分级树中显示了相应的数据节点，如图7-26所示。

3）施加约束条件。

a）选择工具栏中【约束类型】中的【用户定义约束】命令，弹出【UserDefined（1）】对话框，如图7-27所示。【名称】默认为【UserDefined（1）】，在【模型对象】中选择二力杆一端圆孔建立的刚性连接点作为选择对象，在【方向】选项的【位移CSYS】中切换为【圆柱坐标系】，弹出图7-28所示的对话框，将【类型】切换为【对象的CSYS】。在窗口中单击该端圆孔的外环周边，即可建立一个圆柱坐标系，在相应模型上出现了该坐标系的符号，如图7-29所示。

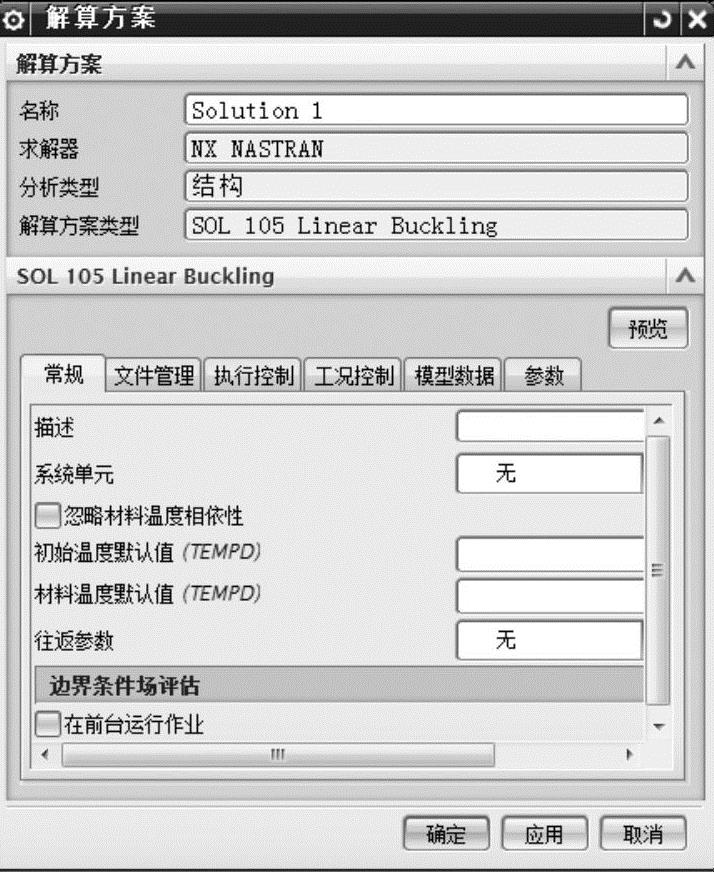
图7-25 建立线性屈曲的解算方案

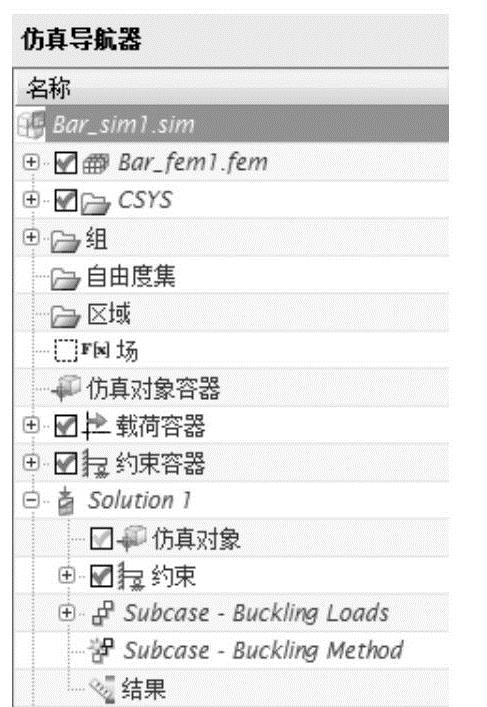
图7-26 建立仿真模型后的节点

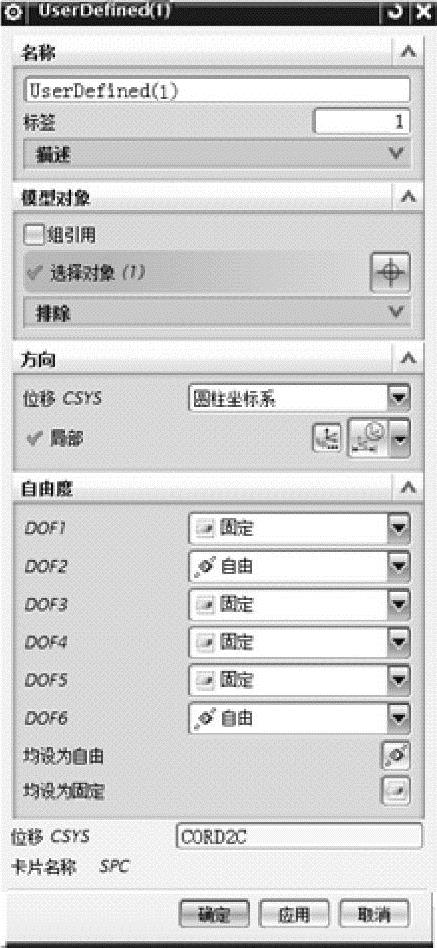
图7-27 一端圆孔刚性连接的约束设置

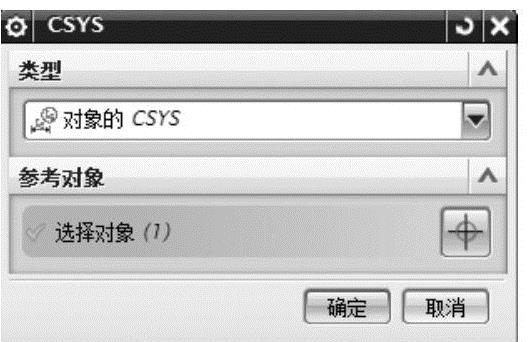
图7-28 局部圆柱坐标系的设置

b）【自由度】选项的【DOF2】和【DOF6】默认为【自由】，其他4个自由度切换为【固定】，单击【应用】按钮，完成二力杆一端圆孔刚性连接约束的定义。

c）按照上述的方法和操作步骤，参照图7-30进行相关选项的设置，完成二力杆另一端圆孔刚性连接约束的定义。

4）施加载荷。

单击工具栏中的【载荷类型】按钮右侧的下拉按钮，在下拉菜单中选择【力】命令，弹出【Force（1）】对话框，如图7-31所示，【名称】默认为【Force（1）】，【类型】选项保留默认设置，在【模型对象】中选择二力杆一端圆孔建立的刚性连接点作为【选择对象】，在【力】文本框中输入【1000】，单位默认为【N】，选择【指定矢量】选项，选择【-ZC】方向，单击【确定】按钮，完成屈曲分析作用载荷的定义，载荷施加效果如图7-32所示。

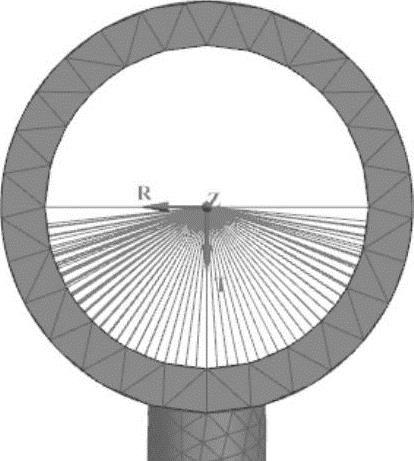
图7-29 局部圆柱坐标系的设置结果

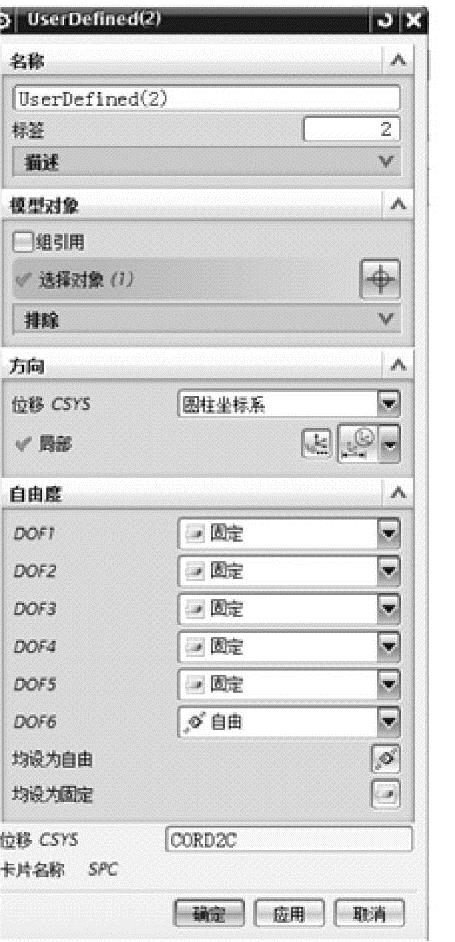
图7-30 另一端圆孔刚性连接的约束设置

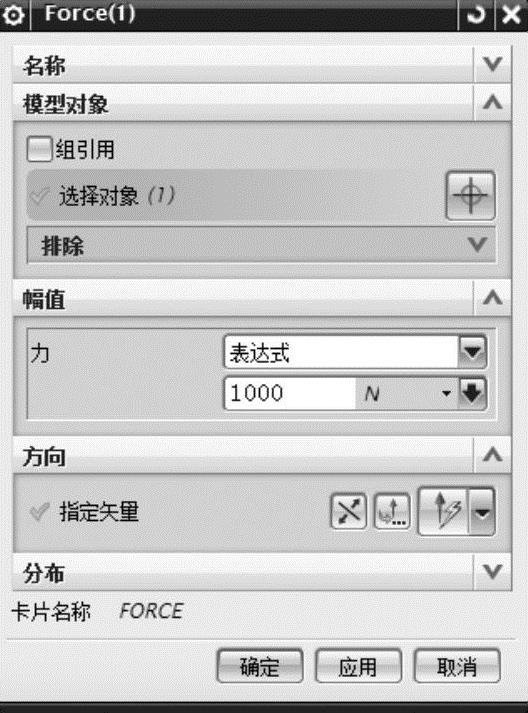
图7-31 【Force（1）】对话框

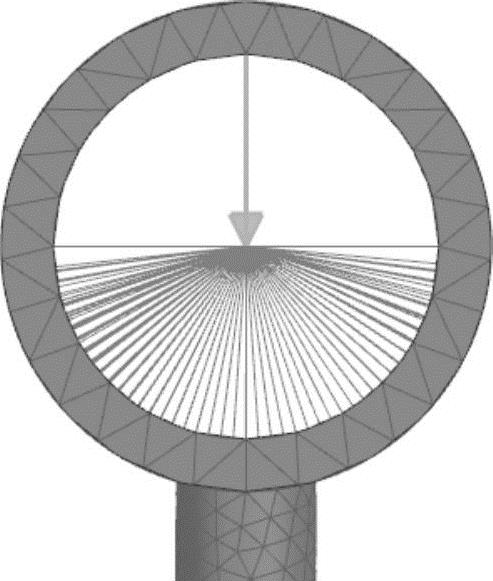
图7-32 载荷施加的结果

提示

在线性屈曲分析中，如果要得到屈曲失稳载荷，载荷施加的大小并不是很重要，可以为单位载荷或具体数值；在UG NX 8.5高级仿真中，在子工况【Subcase-Buckling Loads】可以定义具体的载荷，在分析结果中可以得到该载荷的线性静力分析；在子工况【Subcase-Buckling Method】可以得到屈曲分析的特征值，将得到的特种值与施加的载荷相乘即得到相应的屈曲失稳载荷。

（3）线性屈曲响应仿真模型的求解

1）在【仿真导航器】窗口的分级树中，单击图7-26所示的【Solution1】节点下的子工况【Subcase-Buckling Loads】节点，弹出图7-33所示的【解算步骤】对话框，可以对临界纵向载荷进行编辑和定义，本实例默认对话框中的所有参数。

2）右击图7-26所示的子工况【Subcase-Buckling Method】节点，从弹出的快捷菜单中选择【激活】命令，再次右击该节点并从弹出的快捷菜单中选择【编辑】命令，弹出图7-34所示的【解算步骤】对话框，可以对屈曲方法进行定义和编辑。在对话框中单击【Lanczos数据】右侧的【编辑】按钮，可以对得出的屈曲特征值的模态数进行编辑。

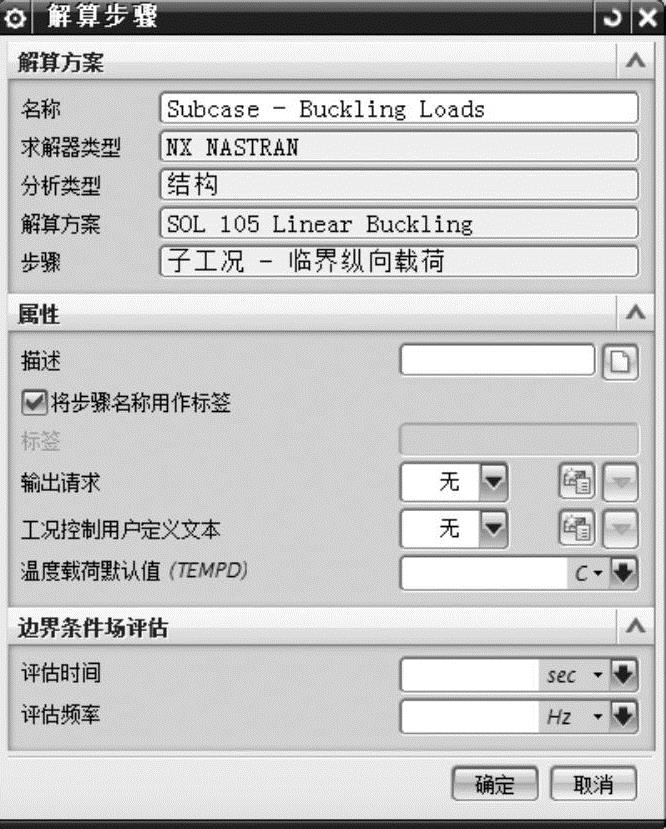
图7-33 子工况屈曲临界纵向载荷定义

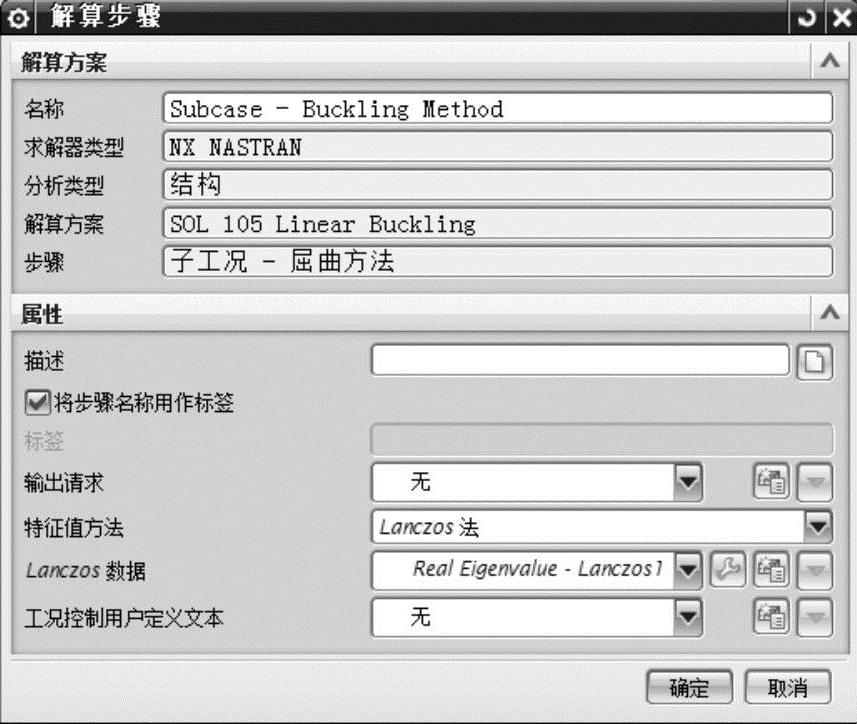
图7-34 子工况屈曲方法定义

3）右击【Solution 1】节点，从弹出的快捷菜单中选择【求解】命令，弹出【求解】对话框，单击【确定】按钮。

4）依次出现【模型检查信息】、【分析作用监视器】和【解算监视器】3个对话框，其中【解算监视器】包括【解算方案信息】、【稀疏矩阵求解器】和【特征值抽取】3个选项卡。等待出现【作业已完成】的提示信息后，关闭各个信息对话框。双击出现的【结果】节点，进入后处理分析环境。

（4）屈曲计算结果的查看

1）在【后处理导航器】窗口展开【Solution1】节点，其中包括【Subcase-Bulking Loads】和【Subcase-Bulking Method】2个子节点，展开【载荷工况2】各个子节点，如图7-35所示。可以查看子工况【Subcase-Bulking Loads】下的屈曲载荷作用下结构的位移及应力情况，以及子工况【Subcase-Bulking Method】下的屈曲失稳的特征值及相应的屈曲失稳形式。

2）单击展开子工况【subcase-Bulking Loads】下的相应子节点，打开【位移-节点的】，双击【Z】节点，如图7-36所示；双击【位移-节点的】下的【幅值】节点，图7-37所示，即为结构在1000N载荷下的整体变形情况。双击【应力-单元的】下的【VonMises】节点，图7-38所示，即为结构在1000N载荷下的Von Mises应力情况。

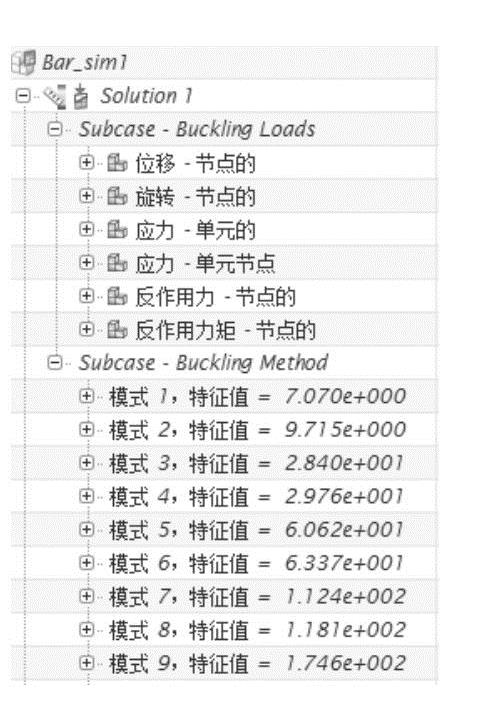
图7-35 Solution 1节点子工况结果列表

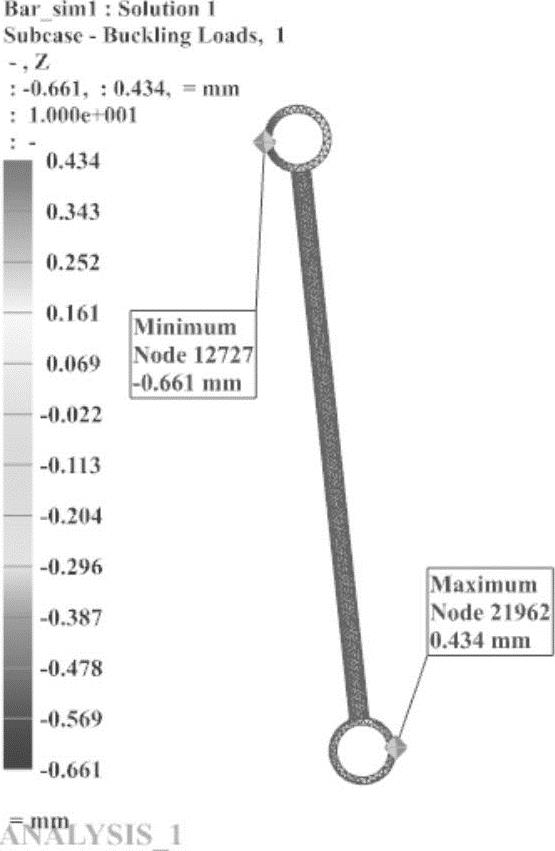
图7-36 结构在屈曲载荷载荷下的Z向位移结果

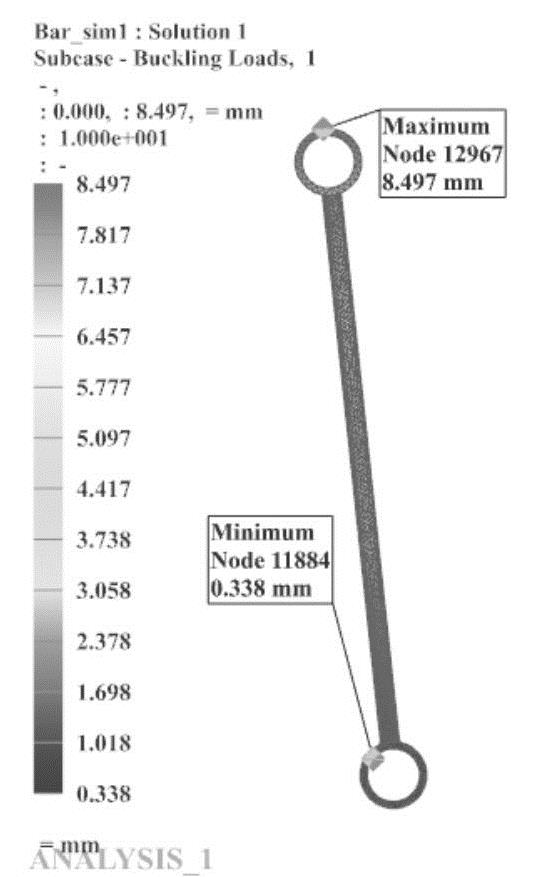
图7-37 结构在1000N载荷下的整体变形情况

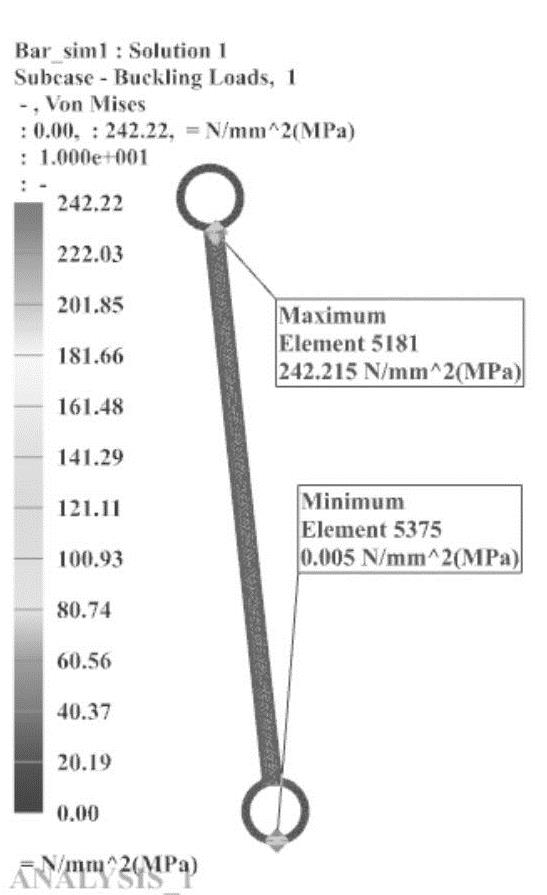
图7-38 结构在1000N载荷下的Von Mises应力情况

3）单击展开子工况【subcase-Bulking Method】下的相应子节点，可以查看分析得到的特征值情况。从图7-35可以看出：第1模式对应的临界载荷为7070N（1000N×7.07），第2模式对应的临界载荷为9715N（1000N×9.715）。展开【模式1，特征值=7.07】节点下的【位移-节点的】，双击【Z】，得到特征值为7.07情况下的Z向位移的屈曲失稳形式，如图7-39所示；双击【幅值】，得到特征值为7.07情况下结构整体的屈曲失稳形式，如图7-40所示；双击【应力-单元的】节点下的【VonMises】，得到特征值为7.07情况下结构整体的Von Mises应力情况，如图7-41所示；打开【模式2，特征值=9.715】节点下的【位移-节点的】，双击【幅值】，得到特征值为9.715情况下结构整体的屈曲失稳形式，如图7-42所示。

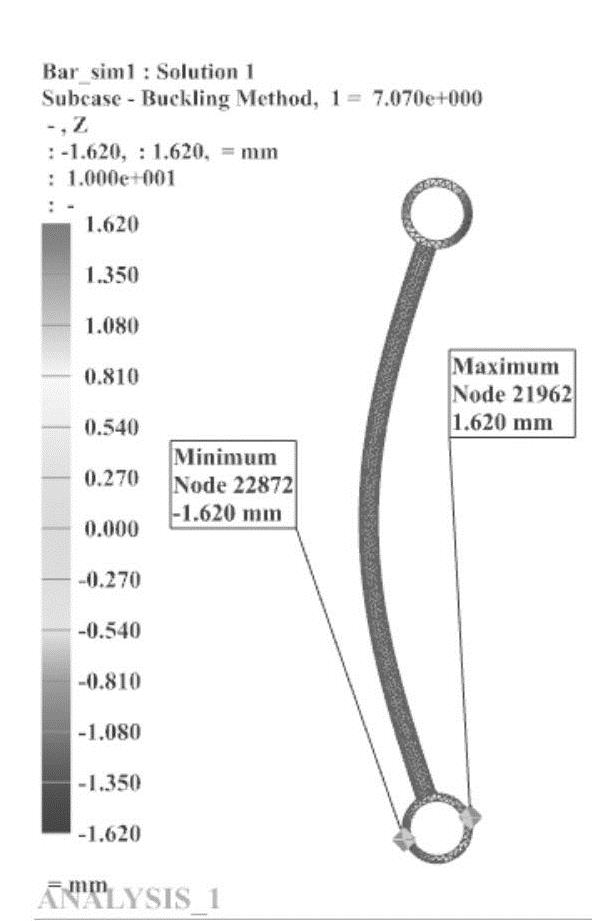
图7-39 特征值为7.07情况下的Z向位移的屈曲失稳形式

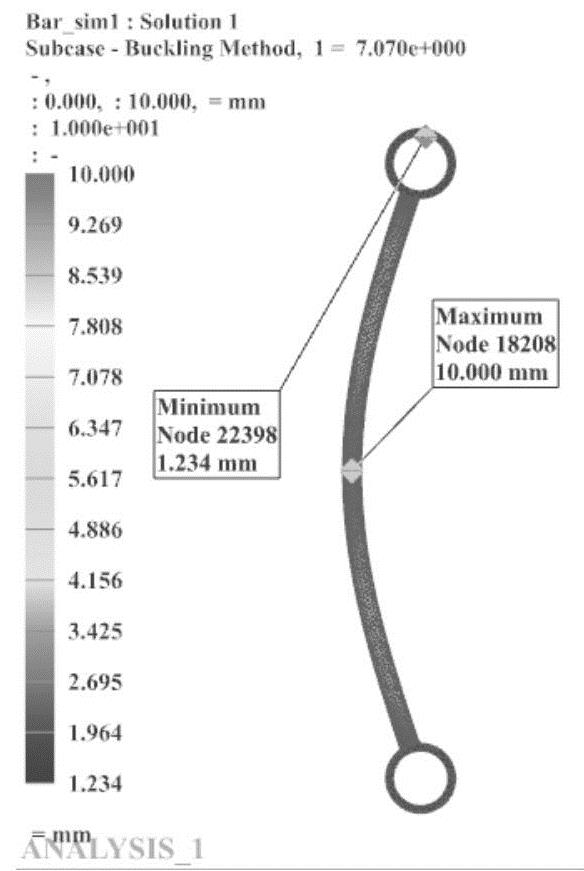
图7-40 特征值为7.07情况下的整体屈曲失稳形式

图7-41 特征值为7.07情况下的整体Von Mises应力情况

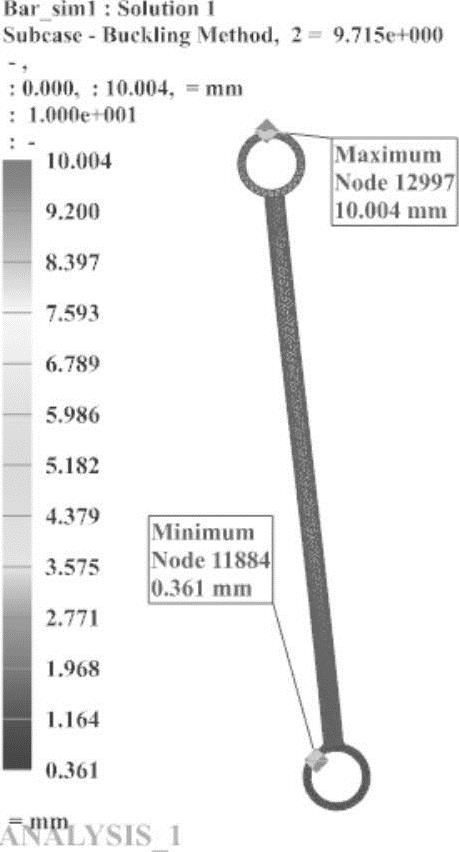
图7-42 特征值为9.715情况下的整体屈曲失稳形式

4）查看每一个模式的屈曲失稳形式及应力情况，可以单击工具栏中的【动画】按钮来查看结构的动态失稳情况，弹出的【动画】对话框如图7-43所示。将【动画】选项切换为【迭代】，【开始载荷工况】、【结束载荷工况】和【结束迭代】选项保留默认设置，单击【播放】按钮。演示出10个模式的失稳形状连续变化过程后，退出动画演示功能。

5）保存计算结果，单击工具栏中的【返回到模型】按钮，退出【后处理】显示模式，完成后处理分析结果的查看。

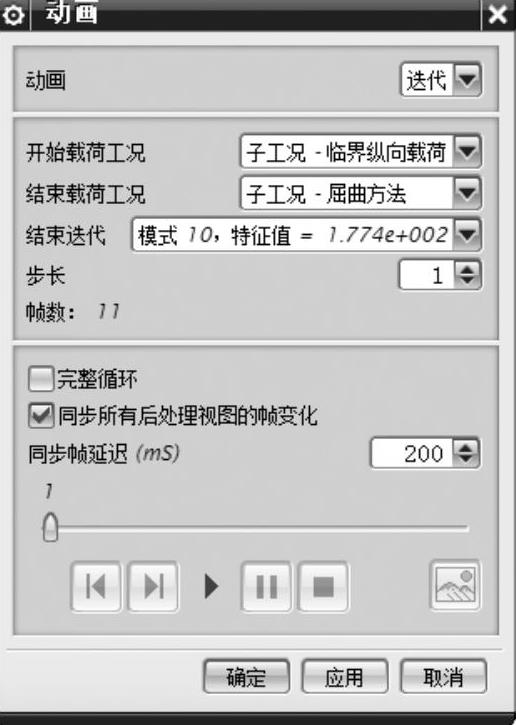
图7-43 【动画】对话框

提示

对于同一个结构模型，结构屈曲响应的特征值结果与屈曲失稳形状和作用载荷的大小无关，在一定的范围内，其特征值对应的失稳形状一般不发生变化，但是结构形状和尺寸的变化达到一定范围后，不仅仅结构的特征值会变化，失稳形态也会发生变化。

从上述分析解算结果来看，当作用载荷超过弹变范围后或分析得出的应力结果超出了材料的屈服极限，线性弹性静态解算结果不能反映实际变形情况，而需要采用非线性静态解算来模拟实际状况。

本实例中其他计算结果和显示模式请参考随书光盘Book_CD\Part\Part_CAE_Finish\Ch07_Bar\文件夹中的相关文件，操作过程的演示请参考视频文件Book_CD\AVI\Ch07_Bar.AVI。

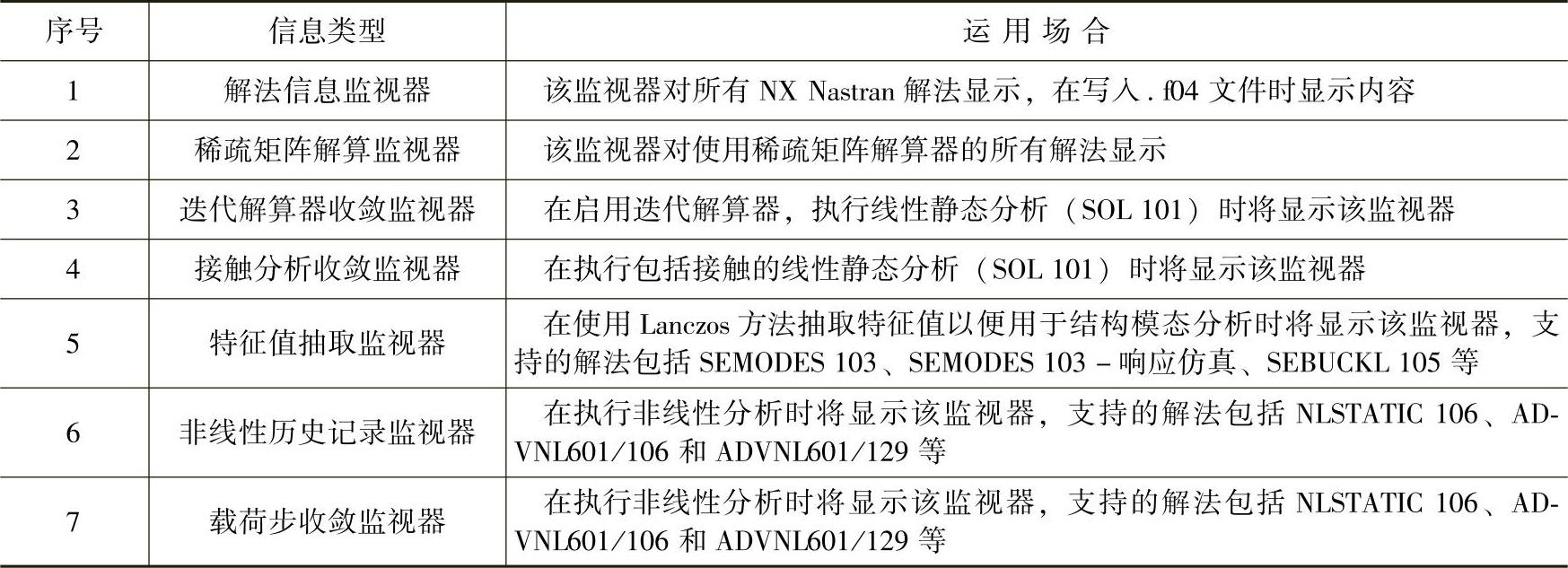
最后简单说明一下利用解算监视器查看相关信息方面的内容。在成功写入待解算文件后，解算监视器将显示有关当前解算进度的实时信息，可以监视解法是否收敛，估计解算所需的剩余时间等，所显示的信息取决于模型参数设置和解算类型。表7-1所示为解算监视器常见的信息类型及其运用场合。

表7-1 解算监视器的信息类型及其运用场合

（5）线性屈曲仿真分析与理论计算比较

按照本例中所使用的约束形式，立杆失稳临界载荷的计算公式见公式7-3（两端铰支连接的梁的屈曲临界载荷计算公式参考《材料力学》第四版，刘鸿文著），分析结果与NX Nastran计算结果的对比如表7-2所示。可见误差可以控制在3%以内，误差原因是没有考虑二力杆两端圆孔形状和大小对整体屈曲响应计算结果的影响，验证了分析结果的准确性。

表7-2 分析结果与理论计算结果的第一阶临界失稳载荷对比