受一定载荷（以压载荷为主）作用的结构（常指薄壁或者细长类杆/轴/桁架等整体刚度相对较弱的结构）处于稳定的平衡状态，当载荷达到某一值时，再增加微小增量，则结构的平衡位置将发生很大的变化，结构由原来的平衡状态经过不稳定的平衡状态而达到一个新的稳定平衡状态。这一过程就是结构失稳或屈曲，相应的载荷称为屈曲载荷或临界载荷。
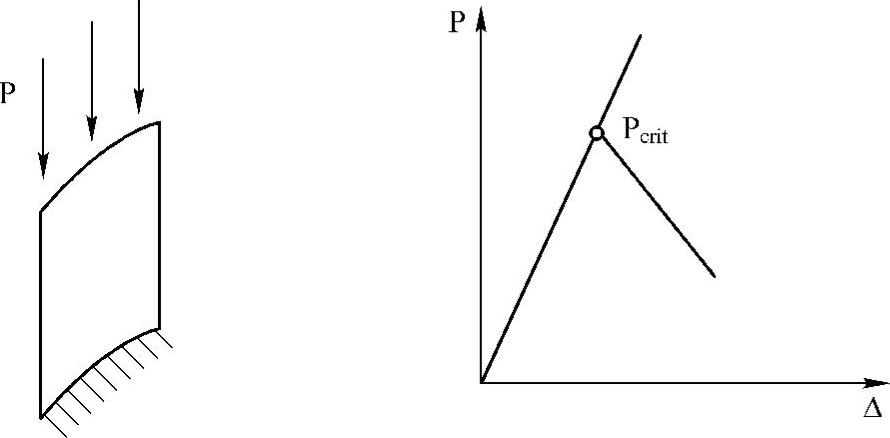
在实际中，屈曲主要表现为两种形式：快速通过（Snap-Through）失稳和分叉（Bifur-cation）失稳。快速通过失稳形式表现为从一个平衡位置快速通过，跳跃到另一个平衡位置，也称为后屈曲，如图7-1所示。除此之外，结构在局部高压应力作用下的起皱和表面重叠现象也是一种局部失稳形式。另一种失稳形式常用分叉来描述，失稳出现在两个或多个平衡路径的交点，交点即为分叉点，表征屈曲失稳的初始位置，如图7-2所示。
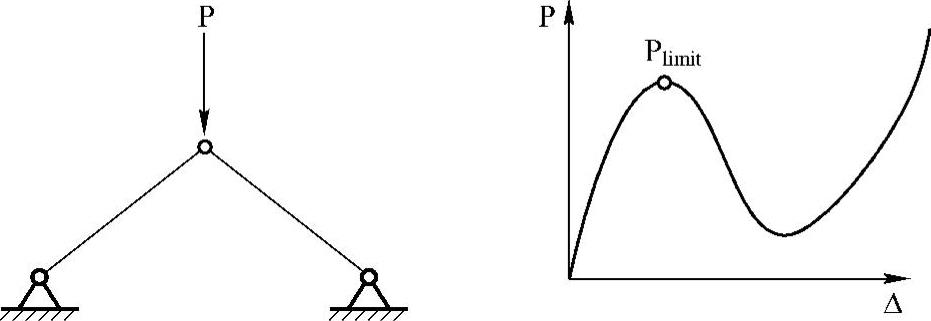
图7-1 快速通过失稳示意图
采用有限元软件分析屈曲可以确定结构开始变得不稳定时的临界载荷和屈曲模态形状。目前，对屈曲问题的分析大致有两类：一类是通过特征值分析计算屈曲临界载荷，根据是否考虑非线性因素对屈曲载荷的影响，这类方法可细分为线性屈曲分析和非线性屈曲分析；另一类是利用综合Newton-Raphson迭代的弧长法来跟踪确定加载方向，跟踪失稳路径的增量，非线性方法能有效地分析非线性屈曲和失稳问题。
(www.xing528.com)
图7-2 分叉失稳示意图
线性屈曲分析可用于预测一个理想弹性结构的理论屈曲强度，相当于《材料力学》教材中的弹性屈曲分析方法。但是，由于结构初始缺陷和非线性使得很多问题的屈曲行为实际上不在弹性屈曲强度处发生，因此特征值屈曲分析的计算结果相对保守，采用非线性屈曲分析则可以有效模拟实际的失稳现象。
屈曲分析在实际工程中有着广泛的应用，如汽车底盘的转向拉杆、多连杆式悬架中的控制臂、制动操作机构中的踏板臂、建筑桥梁行业中使用的屈曲约束支撑、大型钢结构（如塔式起重机、游乐设备）细长构件、汽车覆盖件蒙皮等都需要作屈曲失效分析。实际工程中多采用线性屈曲分析，非线性屈曲分析（也称为后屈曲分析）由于比较复杂，应用不多，但在飞机蒙皮等项目分析中有着深入的应用。
从软件操作角度看，线性屈曲分析是非线性屈曲分析的基础，并且在进行非线性屈曲分析之前可以利用线性屈曲分析，先了解屈曲模态形状，预测屈曲载荷的上限。因此，本实例只针对第一种方法中的屈曲问题进行分析和讨论，采用UGNX高级仿真提供的【SOL 105 Linear Buckling】特征值屈曲解算功能，介绍其操作流程和运用方法，为进行后续的非屈曲分析打下基础。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
