案例五：非线性规划解析

客观世界中的大部分问题都是非线性的，一般情况下可以利用线规划性的知识将非线性的问题转化为线性问题。但在实际问题中，有一些是不能进行线性化处理的，否则将严重影响模型对实际问题近似的可依赖性。由于非线性规划问题在计算上常是困难的，理论上的讨论不能像线性规划那样给出简洁的结果形式和全面透彻的结论。这点又限制了非线性规划的应用，所以，在数学建模时，要进行认真的分析，对实际问题进行合理的假设、简化，首要考虑线性规划模型，若线性近似误差较大时，则考虑用非线性规划。

例9　某公司有6个建筑工地要开工，每个工地的位置（用平面坐标系a，b表示，距离单位：千米）及水泥日用量d（吨）由下表给出。目前有两个临时料场位于A（5，1），B（2，7），日储量各有20吨。假设从料场到工地之间均有直线道路相连。1）试制定每天的供应计划，即从A，B两料场分别向各工地运送多少吨水泥，使总的吨千米数最小。2）为了进一步减少吨千米数，打算舍弃两个临时料场，改建两个新的，日储量各为20吨，问应建在何处，节省的吨千米数有多大？

表4-8　工地位置（a，b）及水泥日用量d

（1）分组

（2）设计问题

针对本题目，教师可以先布置关于非线性规划的基本问题：1）非线性规划问题的标准形式、可行解、局部最优解和全局最优解？2）非线性规划模型求解的基本思路？然后再设计关于本题的问题：3）第一小问是线性规划还是非线性规划，目标函数如何选取？4）改建两个新料场时的问题是线性规划还是非线性规划问题，目标函数如何取？

（3）引导学生完成任务

由于非线性规划的问题难度较大，一般先引导学生按照题目要求先给出目标函数：

约束条件如下：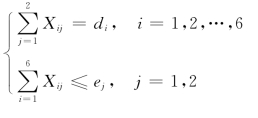

在引导学生针对使用临时料场时，建立新的目标函数：，j）Xij，并给约束条件：

其中，为常数。(www.xing528.com)

设X11=X1，X21=X2，X31=X3，X41=X4，X51=X5，X61=X6 X12=X7，X22=X8，X32=X9，X42=X10，X52=X11，X62=X12，改建两个新料场，要同时确定料场的位置（xj，yj）和运送量Xij，在同样条件下使总吨千米数最小。这是非线性规划问题。非线性规划模型为：

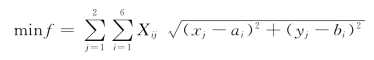
约束条件：

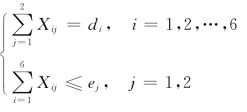
设X11=X1，X21=X2，，X31=X3，X41=X4，X51=X5，，X61=X6　X12=X7，X22=X8，，X32=X9，X42=X10，X52=X11，，X62=X12，x1=X13，y1=X14，x2=X15，y2=X16

（4）成果展示

对所建的模型，采用MATLAB进行求解，得出最终的运料方案如下：

表4-9　运料方案

总的吨千米数为105.4626。比用临时料场节省约31吨千米。

（5）反思问题

这道题目是一个典型的非线性规划问题，在问题反思的阶段要引导学生区分线性和非线性的区别，并对问题进行推广。