线性规划：实践与探索

线性规划是运筹学中研究较早、发展较快、应用广泛、方法较成熟的一个重要分支，它是辅助人们进行科学管理的一种数学方法.在经济管理、交通运输、工农业生产等经济活动中，提高经济效果是人们不可缺少的要求，而提高经济效果一般通过两种途径：一是技术方面的改进，例如改善生产工艺，使用新设备和新型原材料.二是生产组织与计划的改进，即合理安排人力物力资源.线性规划所研究的是：在一定条件下，合理安排人力物力等资源，使经济效果达到最好.一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题。满足线性约束条件的解叫做可行解，由所有可行解组成的集合叫做可行域。决策变量、约束条件、目标函数是线性规划的三要素.

线性规划法是解决多变量最优决策的方法，是在各种相互关联的多变量约束条件下，解决或规划一个对象的线性目标函数最优的问题，即给与一定数量的人力、物力和资源，如何应用而能得到最大经济效益。其中目标函数是决策者要求达到目标的数学表达式，用一个极大或极小值表示。约束条件是指实现目标的能力资源和内部条件的限制因素，用一组等式或不等式来表示。

线性规划法一般采取三个步骤：

第一步，建立目标函数。

第二步，加上约束条件。在建立目标函数的基础上，附加下列约束条件

第三步，求解各种待定参数的具体数值。在目标最大的前提下，根据各种待定参数的约束条件的具体限制便可找出一组最佳的组合。

例5　某商品有m个产地、n个销地，各产地的产量分别为a1，…，am，各销地的需求量分别为b1，…，bn。若该商品由i产地运到j销地的单位运价为cij，问应该如何调运才能使总运费最省？

（1）成立合作小组

首先对学生进行分组，让学生主动去寻找线性规划问题的背景内容，了解线性规划问题，所谓线性规划问题，就是求一组满足一个线性方程组（或线性不等式组）的非负变量的值，使一个关于这组变量的新型目标函数达到最大值或者最小值的问题。这类问题的数学表达式就称为线性规划问题的数学模型。

（2）引入问题

设定如下问题：1）本题是哪种规划类的问题？2）本题中的目标函数是什么？3）约束条件是什么？4）如何求解？

（3）引导学生完成任务

在对规划问题有了初步了解后，可以先建立目标函数：引入变量xij，其取值为

由i产地运往j销地的该商品数量，数学模型为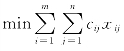，在此引导学生一起寻找约束条件如下：

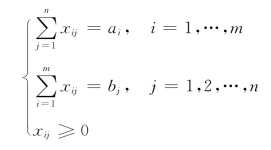
（4）成果展示

在解决实际问题时，把问题归结成一个线性规划数学模型是很重要的一步，但往往也是困难的一步，模型建立得是否恰当，直接影响到求解。而选取适当的决策变量，是我们建立有效模型的关键之一。对产销平衡的运输问题，由于有以下关系式存在：

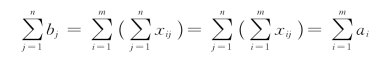(www.xing528.com)

其约束条件的系数矩阵相当特殊，可用比较简单的计算方法，习惯上称为表上作业法。

（5）反思

此时，教师科研和学生一起去复习单纯性法的求解思路，其求解工作在运输表上进行逐步迭代如下：先按某一规则找出一个初始解（初始调运方案）；再对现行解作最优性判断；若这个解不是最优的，就在运输表上对它进行调整改进，得一新解；再判断，再改进，直到得到最优解。

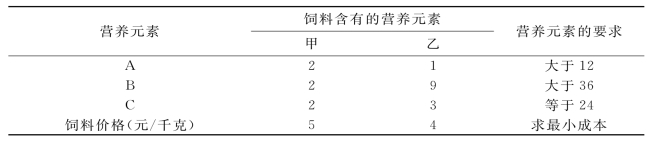
例6　配料问题。

某养鸡场饲养一批小鸡，对小鸡健康厂长的基本营养元素有三种，简单地称为A、B、C。这批小鸡每日对这三种营养的最低需要量是：元素A为12单位，元素B为36个单位，而元素C恰好为24个单位，C元素不够或过量都是有害的。现市场供应的饮料有甲、乙两种，甲饲料每千克5元，所含的营养元素A为2个单位，B为2个单位，C为2个单位；乙饲料每千克4元，所含的营养元素A为1个单位，B为9个单位，C为3个单位。养鸡场负责人希望得到甲乙两种饲料的混合饲料的最优配比，即既能满足小鸡健康成长的需要，又能降低饲料的费用。同样，为了方便分析，将上述条件用如下表表示。

表4-6　某养鸡饲料数据表

（1）成立合作小组

（2）教师设计任务

由上面两个例子分别建立了生产模型、配料问题的数学模型，在实际中，还有诸如布局问题、指派问题，这些问题虽然各式不一样，但都是线性规划问题，这都具备有线性规划的特征。通过实例，让学生完成：1）线性规划的一般形式？2）线性规划的标准形式是什么？3）如何将其他形式转换为标准形式？

（3）引导学生完成数学任务

分别引导学生了解图解法、代数法的求解过程。

（4）成果展示

以小组为单位，在交流合作的过程中完成模型求解。

（5）反思

通过模型引入、模型建立以及模型求解过程，通过小组间协作、交流过程，充分发挥学生的主动性，在模型展示的过程中，不断反思，不断改善，在改进的过程中，使学生不断进步。