拓展学生数学建模实践：微分方程案例

微分方程模型是实际问题需寻求某个变量y随另一变量t的变化规律：y=y（t），一般很难直接建立二者之间的关系，但是通过实际问题可以建立未知变量导数的方程，这类问题都属于微分方程模型。

（1）成立合作小组

（2）设定任务，引入问题

首先让学生主动去了解微分方程，设定如下任务：1）什么样的问题可以用微分方程建立？2）微分方程建模的步骤是什么？3）如何将实际问题转化为数学式子？4）如何进行微分方程的求解？

例3　物体冷却问题。

一个较热的物体置于室温为18℃的房间内，该物体最初的温度是60℃，3分钟以后降到50℃。想知道它的温度降到30℃需要多少时间？10分钟以后它的温度是多少？

再次设定任务如下：1）本体所需物理知识是什么？2）本题在采用定律是应该做何种假设？3）通过那句话可以建立数学式子？4）所建立的模型属于微分方程模型吗？5）如何求解模型？

（3）引导学生完成任务

本例所涉及的问题属于微分方程模型，在微分方程建模时，需要搞清楚建模的机理是什么，例如本例可以采用牛顿冷却定律（将温度为T的物体放入处于常温m的介质中时，T的变化速率正比于T与周围介质的温度差）来进行建模，建模中需要假设假设房间足够大，放入温度较低或较高的物体时，室内温度基本不受影响，即室温分布均衡，保持为m。设物体在冷却过程中的温度为T（t），t≥0。由T的变化速率正比于T与周围介质的温度差，翻译为成正比，建立模型如下：

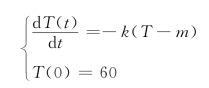
求解模型得到：T（t）=18+42e（1／3ln16／21）t。

（4）展示成果，相互交流

对于上述问题，各个小组将建立的模型进行展示，通过计算可得，该物体温度降至30℃需要8.17分钟。

（5）学习反思

本例中建立的模型是通过物理中的牛顿冷却定律得到的，相应的问题比如，考古文物年份的判定，放射性元素的衰变，药物浓度的变化等等都可以采用这样的丰富求解，要学生学会举一反三。

例4　人口预测问题。

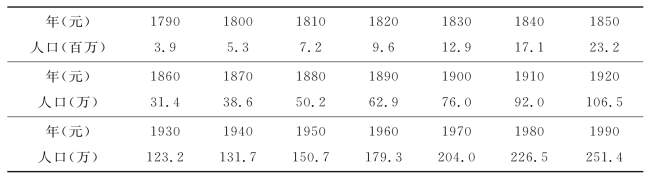
人口问题是当前世界上人们最关心的问题之一。认识人口数量的变化规律，作出较准确的预报，是有效控制人口增长的前提。下面介绍两个最基本的人口模型，并利用表1给出的近两百年的美国人口统计数据，对模型做出检验，最后用它预报2000年、2010年美国人口。

表4-3　美国人口统计数据

（1）成立合作小组

（2）设定任务

在前期了解了微分方程模型的基础上设定如下问题：1）分析影响人口增长的因素：人口基数，出生率与死亡率的高低，人口男女比例，人口年龄组成，工农业生产水平的高底，营养条件，医疗水平，人口素质，环境污染。还涉及到各民族的风俗习惯，传统观念，自然灾害，战争，人口迁移等，对人口增减有很大影响。2）这些因素中那些是非常重要必不可少的？3）建立的模型属于哪一类数学模型？4）建立模型的假设是什么？那些因素可以忽略？

（3）引导学生完成任务(www.xing528.com)

本例所涉及的问题属于微分方程模型，首先可以引导学生回顾银行存钱的例子，建立一个只有人口增长率的简单模型，通过小组之间讨论，验证了模型不合理，参考课本，建立马尔萨斯假设：人口增长率t是常数（或单位时间内人口的增长量与当时的人口成正。记时刻t=0时人口数为t0，时刻t的人口为x（t），由于量大，x（t）可视为连续、可微函数.t到t+Δt时间内人口的增量为：

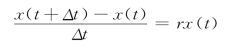
于是x（t）满足微分方程：

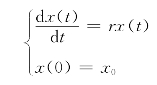
解微分方程得：x（t）=x0ert。

（4）展示成果，相互交流

通过表中1790—1980年的数据拟合得：r=0.307。

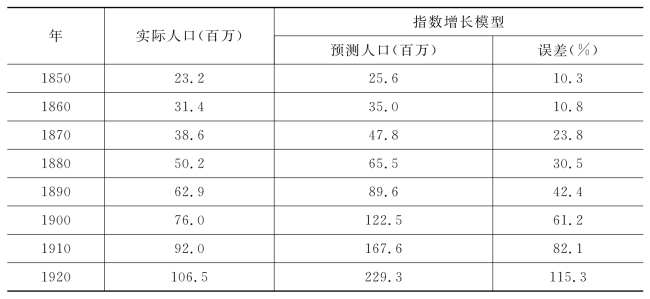
求出用模型预测的1810—1920年的人口数，见表4-4。

表4-4　国实际人口与按指数增长模型计算的人口比较

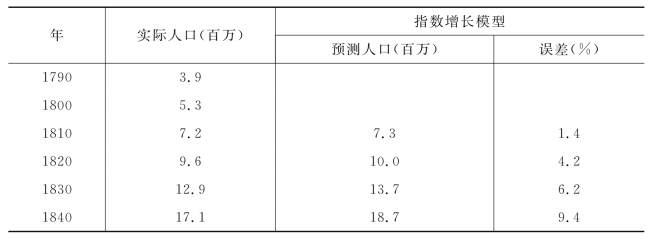
续表

（5）学习反思

本例中建立的模型通过检验发现误差较大，教师科研引导学生进行分析，发现这种模型得到的人口会无限的增长，不符合实际情况，因此可以再次引导学生，布置新的任务：1）人口在增长的时候会无限制的增长吗？2）人口在增长的时候增长率会随着那些因素而递减？

分析原因，发现人口的增加，自然资源、环境条件等因素对人口增长的限制作用越来越显著，如果当人口较少时人口的自然增长率可以看作常数的话，那么当人口增加到一定数量以后，这个就要随着人口增加而减少，于是应该对指数增长模型关于人口净增长率是常数的假设进行修改。最简单假定人口相对增长率随人口的增加而线性减少人口增长率r为人口x（t）的函数r（x）（减函数），r（x）=r-sx，r，s＞0（线性函数），r叫做固有增长率；自然资源和环境条件年容纳的最大人口容量xm。当x=xm时，增长率应为0，即r（xm）=0，于是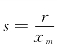，代入r（x）=r-sx得：。

建立新的模型：

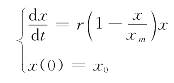
解得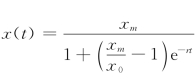；用表中1790—1980年的数据对r和xm拟r=0.2072，xm=464。

表4-5　美国实际人口与按阻滞增长模型计算的人口比较

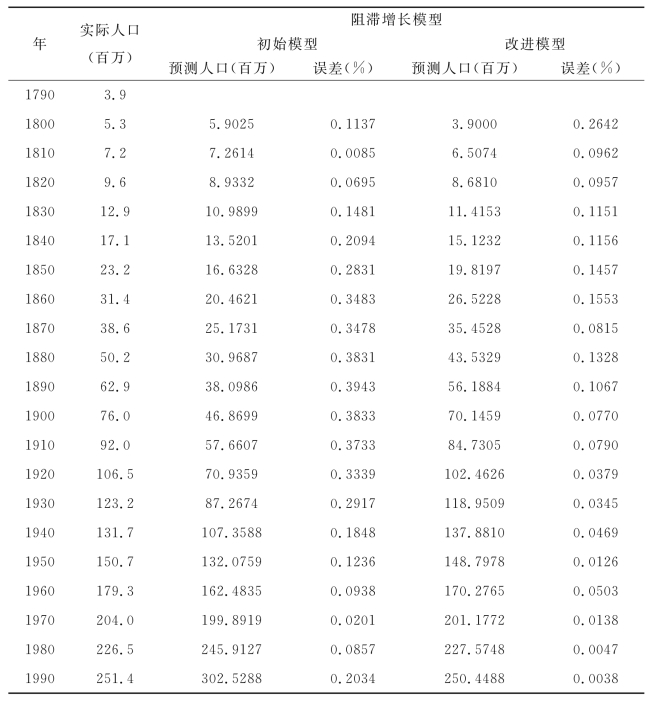
此时通过建立的模型进行再次预测，预测结果发现效果较好。通过本例，教师可以引导学生对于同类问题进行练习，比如，养老金的缴纳问题，都可以采用这种阻滞增长模型进行求解。