支持向量机和目标项目分析的托攻击检测算法

本节分析了基于支持向量机和目标项目分析的托攻击检测算法用到的技术和方法，包括支持向量机、交叉验证和K-最近邻算法，自适应人工合成样本方法Borderline-SMOTE理论等。

（1）支持向量机

支持向量机是一般化线性分类器，可应用于统计分类以及回归分析［112］，并且已经成功应用于模式识别、数据挖掘和文本分类等领域［120，121］。支持向量机通过构造一个分类超平面或者多个超平面用于对数据样本进行分类，这些超平面可能是高维的，甚至可能是无限多维的。在具体的分类任务中，支持向量机的原理是将决策面（超平面）放置在这样的一个位置，其中，两类中接近这个位置的点距离的都最远［122］。以两类线性可分问题为例，如果要在两个类之间画一条线，那么按照支持向量机的原理，先找两类之间最大的空白间隔，然后在空白间隔的中点画一条线，这条线平行于空白间隔。在非线性可分问题中，通过核函数使得支持向量机对非线性样本进行分类。

假如有一些训练数据的正负样本：{xi，yi}，i=1，…，l，yi∈{－1，1}，xi∈Rd，假设有一个超平面H：w·x+b=0，可以将这些正负样本正确地分割开，并且存在两个平行于H的超平面H1和H2：

使离超平面H最近的正负样本刚好分别落在超平面H1和H2上，这些正负样本就是支持向量。其他所有的训练样本都将位于H1和H2之外，也就是满足约束：

w·xi+b≥1 for yi=1

w·xi+b≤-1 for yi=-1

即：

而超平面H1和H2的距离：

VMargin=2/‖w‖

SVM的任务就是寻找一个合适的超平面将正负样本分开，并且使H1和H2的间隔最大。

（2）交叉验证

交叉验证（Cross Validation）是一种将数据样本分成较小子集的方法。先在一个子集上做分析，而再其他子集上做后续对比分析。一开始的子集被称为训练集，剩余的子集则被称为测试集，使用交叉验证可以得到可靠稳定的模型。例如10折交叉验证，将数据集分为10份，轮流将其中9份作训练、1份作测试，将10次计算结果均值作为对算法精度的估计。(www.xing528.com)

（3）K-最近邻法

K-最近邻法［123］是最近邻算法的一个推广应用，对未知样本进行类别决策仅与k个相邻样本有关。K-最近邻法灵活性较好，可与其他模型整合［124］。因此，通常将K-最近邻法与其他分类技术结合以取得更好的分类效果。

（4）自适应人工合成样本方法（Borderline-SMOTE）

传统基于监督学习方法能对平衡数据集进行较好的分类，但在实际应用中数据集标签往往不均衡，这种类不均衡问题会导致分类器过分类结果较差。推荐系统中的托攻击概貌检测其评分数据是典型的不均衡数据集。托攻击概貌占所有概貌的比值往往很低，使用传统的分类方法分类效果很差。在推荐系统托攻击检测中，人们关心的是托攻击类（少数类），因为检测结果中托攻击概貌被误判为真实概貌的代价较高。近年来，学者们在两个方面针对类不均衡问题提出了改进：一是从数据集的角度，通过人工集合少类数据，减小两类数据的差异；另一个是从算法角度解决不均衡问题。本书采用在数据集层面的处理方法改善不均衡数据集。

随机抽样是处理不均衡数据最基本的方法，算法随机选择少数类样本，并将复制的样本添加到少数类中，这就增加了少数类的个数，但是简单地将复制后的数据添加少数类集合中可能使分类器出现过拟合现象。为了解决随机抽样的过拟合问题，Chawla N.V等［125］提出了一种基于人工合成少数类过抽样技术（synthetic minority over-sampling technique，SMOTE）。该算法的基本思想是：首先寻找每一个少数类样本的k个同类最近邻样本（其中k通常是大于1的奇数），然后随机选择k个最近邻中的一个，并在这两个样本之间随机线性插值，构造出新的人工少数类样本。SMOTE方法可以有效地解决分类过拟合问题，而且可使分类器性能得到显著提高。但是由于SMOTE算法对每个少数类样本人工合成相同数量的数据样本，而没有充分考虑边界样本的分布特点，因此使得类间发生重复的概率增加。为了克服上述缺点和不足，近些年一些学者相继提出了许多SMOTE算法的改进。例如文献［126］提出的使用最近邻样本均值点人工合成样本的D-SMOTE算法；文献［127］使用周围空间结构信息的邻居计算公式提出的N-SMOTE过抽样算法。

此外，还有一些自适应过抽样方法相继被提出，代表性的算法包括Borderline-SMOTE算法［128］和自适应合成抽样算法。SMOTE算法为少数类样本集中每一个样本生成人工合成样本，但是非边界样本对分类的作用不大，所以Borderline-SMOTE算法只为那些靠近边界的少数类样本合成样本。

Borderline-SMOTE算法描述如下：设训练样本集为T，少数类样本为F={f1，f2，…，fn}。

①计算少数类样本集F中每一个样本在训练集T中的k个最近邻，然后根据这k个最近邻对F中的样本归类：加入这k个最近邻都是多数类样本则将该样本定为噪声样本，放入N'集合中；反之k个最近邻都是少数类样本则该样本是远离分类边界样本，将其放入S集合中；最后k个最近邻即有多数类样本又有少数类样本则认为是边界样本，存入集合B中。Borderline-SMOTE算法流程如图5.1所示。

图5.1　Borderline-SMOTE算法流程

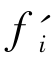②设边界样本集，计算B集合中的每一个样本，i=1，2，…，b在少数类样本F中的k'个最近邻fij并随机选出s（1＜s＜b）个最近邻，计算出它们各自与该样本之间的全部属性的差值dij：dij=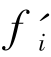－fij，j=1，2，…，s然后乘以一个随机数rij，rij∈（0，1）［如果fij是N集合或S集合中的样本，那么rij∈（0，0.5）］。生成人工少数类样本：

③重复过程②，直到生成人工少数类样本的数目满足均衡样本集的要求，算法结束。