【摘要】:对于多目标优化问题,目标函数是由多个子目标构成的向量。图9-1给出了这两个二维向量之间的4种关系,其中第4种情况无法采用向量自然序进行定义,因此,第4种情况下无法比较大小。2)至少对某一个目标函数使解x′′比解x′好,即存在j,1≤j≤M,使得fi(x′)>fi(x′′)。在一个解集空间P中,没有被其他解所占优的解所构成的集合称为非劣解集,记为P′。
对于多目标优化问题,目标函数是由多个子目标构成的向量。比较两个解的优劣,就需要比较这两个向量的大小,这可以通过定义向量的自然序来实现。以向量a=(a1,a2)和b=(b1,b2)两个二维向量为例,表9-1定义了它们之间的大小关系。图9-1给出了这两个二维向量之间的4种关系,其中第4种情况无法采用向量自然序进行定义,因此,第4种情况下无法比较大小。
表9-1 向量自然序的定义(以二维向量为例)

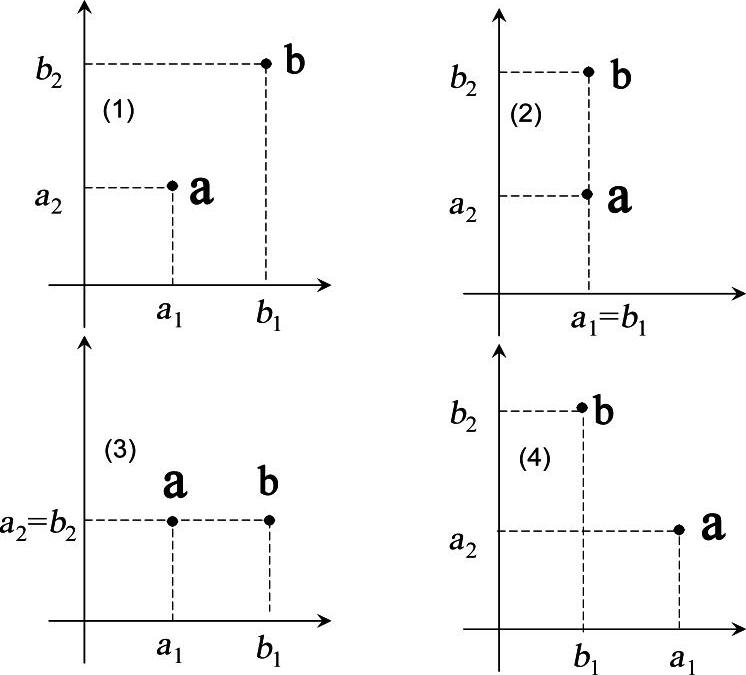
图9-1 两个向量之间的大小比较
把向量的自然序的概念引入到多目标问题中,就可以得到多目标优化问题的两类关系:占优关系和不可比较关系。
当如下两个条件都满足时,称解x′对解x′′占优:(https://www.xing528.com)
1)对于所有的目标函数,解x′都不必解x′′差,即有fm(x′)≤fm(x′′),m=1,2,…,M。
2)至少存在一个目标函数使解x′比解x′′好,即存在i,1≤i≤M,使得fi(x′)<fi(x′′)。
对于如下情况,则称解x′和解x′′无法比较:
1)至少对某一个目标函数使解x′比解x′′好,即存在i,1≤i≤M,使得fi(x′)<fi(x′′)。
2)至少对某一个目标函数使解x′′比解x′好,即存在j,1≤j≤M,使得fi(x′)>fi(x′′)。
在一个解集空间P中,没有被其他解所占优的解所构成的集合称为非劣解集,记为P′。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




