静止均质与线性密度分层环境下的二维浮射流

若浮射流是从长方形孔口射出，在宽度方向上孔口的尺寸比厚度方向大得多，则浮射流可看作二维流动，所以只要沿宽度方向取单位宽度来研究即可。

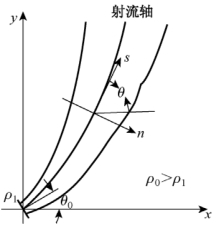
图6－12　静止均质环境中二维浮射流

对二维浮射流的分析，与轴对称性质圆形浮射流的基本原则和方法完全一样，只是具体的数学表达式有所不同。轴对称性质圆形断面浮射流，在对任何变量沿断面积分时，微分方程面积为环形面积，积分变量为半径r，二维浮射流的变量在断面上积分时，其微分单元面积为矩形面积，积分变量为射流厚度方向的长度变量。由于基本假定、基本原理和分析方法都与圆形浮射流完全一样，这里的叙述尽量从简，许多地方只写出其结论。

1．静止均质环境中二维浮射流

（1）基本方程式

如图6－12所示，令垂直于射流轴的横断面上沿厚度方向（从轴线算起）的坐标变量为n，对均质环境下的二维浮射流基本方程式表达如下：

①连续性方程

代入高斯分布函数后积分得

式中q为单宽流量，其余符号同前。

②x方向的动量守恒

积分后得

③y方向的动量方程

④密度差通量守恒方程

⑤含有物质量守恒方程

⑥射流轴线几何特性

以上共七个方程，七个未知数，求解的初始条件为

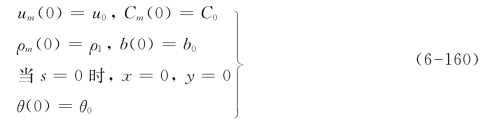
（2）方程组无量纲化

定义下列无量纲变量

无量纲流量

无量纲动量

无量纲坐标

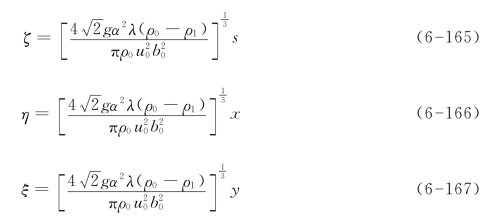
引入上述无量纲变量后，方程组变为

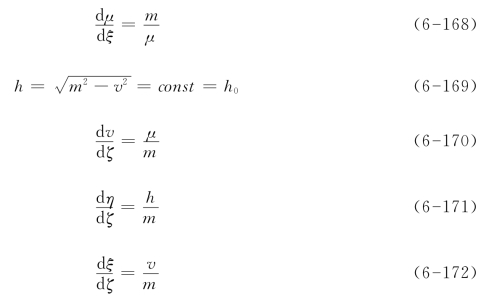
相应的初始条件变为

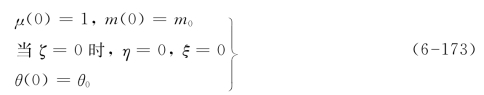
（3）数值解

仍以θ0和m0为参数，数值解的结果整理为两种图解曲线，图的作法和前面介绍的均质环境相同。

在二维浮射流情况下有

轴线上稀释比S0＝C0／Cm＝μ

对二维浮射流的数值解成果是采用α＝0．16，λ＝0．89得出的，这是利用二维浮力羽流的实验成果。

（4）关于初始段的修正

①初始段末端射流半厚度b0

令孔口厚度为B，初始段末端浮射流半厚度

(www.xing528.com)

②以射流孔中心为原点的轴线轨迹坐标

初始段长度5．2B是Albertson等人对二维浮射流的研究成果。

③轴线稀释比

以孔口断面浓度为参考浓度的稀释比

利用上面公式计算稀释比，当采用λ＝0．89时会得出初始段末端断面浓度大于孔口断面浓度的矛盾。因而建议对S的计算应根据S0的大小，区别为两种不同情况：

当S0≥1．06时，

当S0＜1．06时，

④

2．线性密度分层环境中的二维浮射流

（1）基本方程

连续性方程、x方向的动量方程、含有物质量守恒方程以及浮射流轴线轨迹的几何特性与均质环境二维浮射流完全一样。

y方向的动量方程、因为环境密度ρa为变数且与ρ0不等，故应改为下式

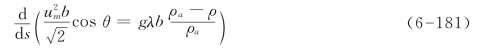
浮力通量不再守恒，其方程式变为

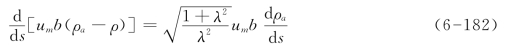
求解方程的初始条件和均质环境二维浮射流的条件式（6－173）一样。

（2）方程组无量纲化

无量纲变量表达式为：

无量纲流量

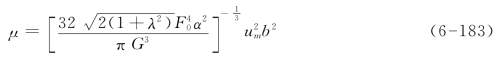
无量纲动量

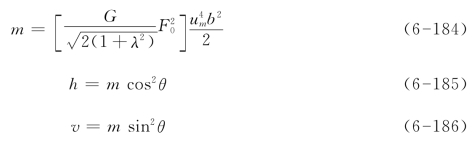
无量纲浮力

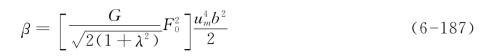
无量纲坐标

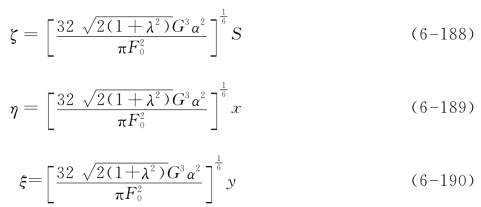
上式中G和F0具有量纲，其定义为

引入上述无量纲变量后微分方程变为

相应的初始条件和均质环境浮射流的初始条件式（6－173）一样。

（3）数值求解

问题的参数为μ0、m0和θ0，图的作法和前面介绍的均质环境相同。

（4）关于初始段的修正

①初始段末端射流半厚度b0

令孔口厚度为B，初始段末端浮射流半厚度

②初始段末端断面的m0及μ0值

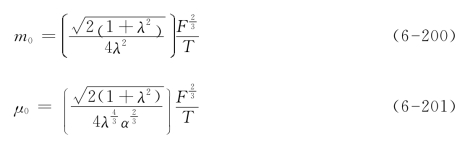
③稀释比