圆管紊流中的离散改进成果

圆管紊流中，在扩散的初始阶段质点的速度变化不是平稳过程，它与质点的起始位置有关，随着时间的推移，历史的关系逐渐不起作用而成为平稳过程，紊流中离散的分析可和层流的离散相比拟而得到解决。

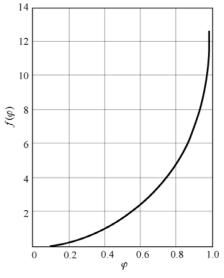
图4－4　均匀圆管紊流的流速分布函数图

当扩散时间足够长时，可以认为纵向离散与径向紊动扩散相平衡，和层流的分析相似，可以写出它们的关系式，纵向离散是纵向流速在断面上的分布不均匀所引起的，紊流的流速分布和层流不同，径向扩散是紊动扩散，性质也和层流不同，所以分析上与层流的区别在于紊流的流速分布和紊动扩散系数的确定。

假定断面流速分布采用

有许多学者对f（φ）进行了研究，泰勒直接采用了斯坦顿和尼古拉斯的测量成果，如图4－4所示。

利用流速分布公式（4－30）得到圆管紊流的断面平均流速V为：

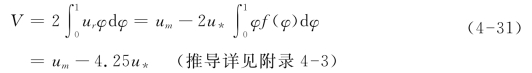
在恒定均匀管道紊流中，，

将式（4－30）、（4－32）代入式（3－29），得到

其中

假定扩散时间增加足够长后，纵向离散与径向紊动扩散保持平衡，忽略沿纵向的紊动扩散项，把固定坐标x改为以平均流速V移动的动坐标ξ，以式（4－19）为基础，以紊动扩散系数E代替分子扩散系数D，令，则式（4－19）

成为

将式（4－33）代入上式，得

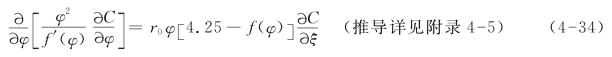
任意点时均浓度由断面平均浓度和二者之间的差值组成，则设C＝Ca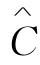＋，假定，同时假设，则，式（4－34）成为

积分（4－35）得(https://www.xing528.com)

或

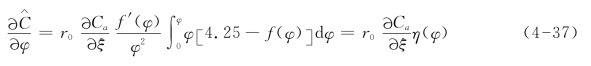
其中

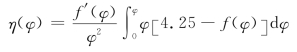
积分（4－37）得

其中，积分式可由流速分布关系求得。

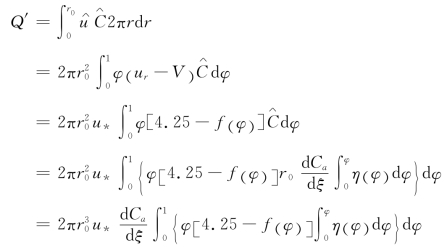
其中可通过数值积分求得其值为－5．03。

于是

通过单位面积的物质扩散通量为：

于是圆管紊流的纵向离散系数为

以上推论中未考虑纵向紊动扩散，根据泰勒求得的纵向紊动扩散系数为

则综合扩散系数为

E≪EL，说明纵向紊动扩散远小于纵向离散作用。