【摘要】:时间连续点源可以看做是无限多瞬时点源mdτ的迭加,m为单位时间投放物质的强度,同样采用动坐标系,引用纯扩散的时间连续点源的积分式令则当τ=0时,;τ=t时,ξ=∞。将上述关系代入式得令,若时间的积分限t→∞,则→0,故式变换为式中,称为β函数。故时间连续点源三维移流扩散的浓度公式为图2-12画出了在均匀流场中仅有x方向纵向流速u的等浓度分布,横纵坐标分别采用无量纲坐标及,浓度值是采用无量纲浓度。
时间连续点源可以看做是无限多瞬时点源mdτ的迭加,m为单位时间投放物质的强度,同样采用动坐标系,引用纯扩散的时间连续点源的积分式
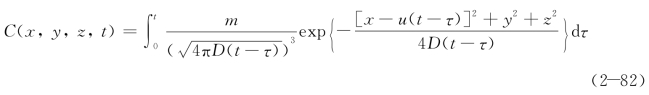
令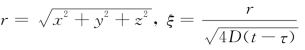
则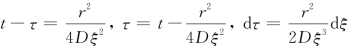
当τ=0时,![]() ;τ=t时,ξ=∞。
;τ=t时,ξ=∞。
将上述关系代入(2-82)式得
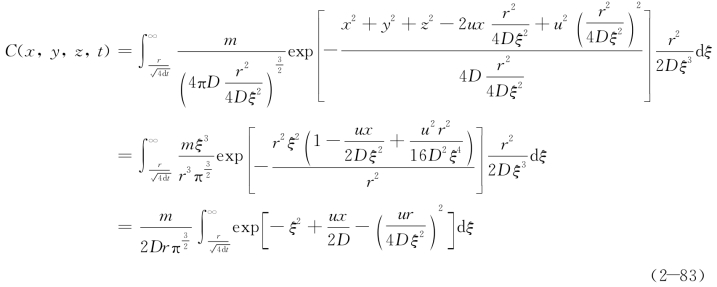
令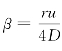 ,若时间的积分限t→∞,则
,若时间的积分限t→∞,则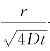 →0,故式(2-83)变换为
→0,故式(2-83)变换为
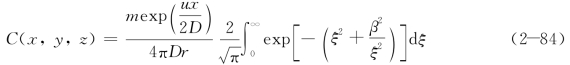
式中,
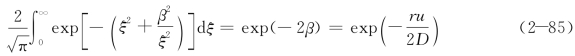
称为β函数。故时间连续点源三维移流扩散的浓度公式为
![]()
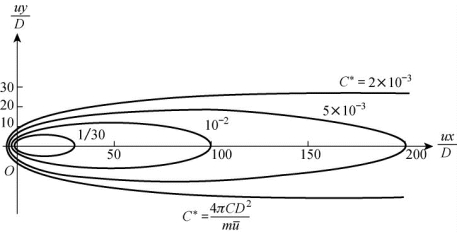
图2-12画出了在均匀流场中仅有x方向纵向流速u的等浓度分布,横纵坐标分别采用无量纲坐标![]() 及
及![]() ,浓度值是采用无量纲浓度
,浓度值是采用无量纲浓度![]() 。
。
图示说明,由于移流作用,沿流动方向把等浓度线拉成了细长形,在点源下游较远处的区域,式(2-86)中r值可以下列近似关系代替
![]()
由于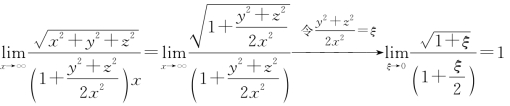
 (https://www.xing528.com)
(https://www.xing528.com)
图2-12 时间连续点源三维扩散的等浓度线
或![]() 及r≈x
及r≈x
从而时间连续点源三维移流扩散的浓度公式(2-86)可以用下面简化公式代替
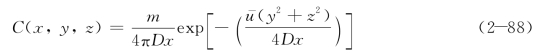
时间连续线源二维移流扩散方程的解为:
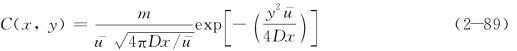
时间连续面源一维移流扩散方程的解为
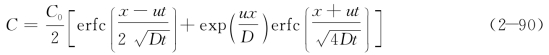
例2-7 三维移流扩散方程如式(2-88)所示,在y=0平面上作出一条![]() ,C*=0.01的等浓度曲线。
,C*=0.01的等浓度曲线。
解:将式(2-88)改写为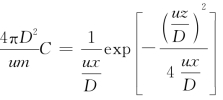
令无量纲浓度![]() ,原式变为
,原式变为
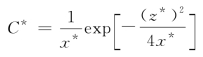
取C*=0.01,然后得上式x*与z*的关系数值,如下表所示,并绘出该等浓度线,如例图所示。

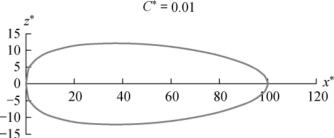
例2-7图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




