时间连续点源的一维扩散，环境水力学

时间连续点源沿一维空间（x方向）扩散，将坐标原点O取在点源中心，初始时刻整个轴上（除O点）浓度为零，在x＝0处浓度突然增加到C0，而随时间延长，在x＝0处浓度一直保持不变，推求时间连续源引起的浓度分布函数C（x，t）。本问题仍当应用一维扩散方程

初始条件t＝0，C｜｜x｜＞0＝0，C｜x＝0＝C0

边界条件x＝0，C｜t＞0＝C0

由量纲分析，组成无量纲变量，并假定解具有如下形式：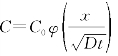

C0为恒定时间连续源的投放浓度（C0＝常数），φ为变量的待定函数。

令，则C＝C0φ（ξ），

而

将上式带入式（2－61）得

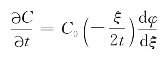
而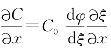，则

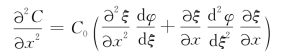
由于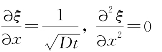

故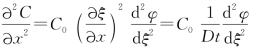

代入一维扩散方程，化简后得到

经过变换后把扩散方程变成了常微分方程，求解方程所要满足的边界条件为x＝0，φ＝1；x＝∞，φ＝0。

因为扩散具有对称性，C（－x，t）＝C（x，t），只需要考虑x正方向即可。

解得

推导过程详见附录2－4。

按照式（2－64）以t为参数画出相对浓度C／C0沿x轴分布如图2－10所示。(www.xing528.com)

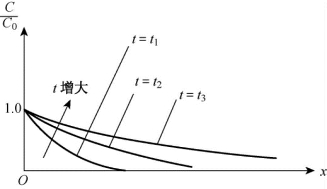
图2－10　相对浓度C／C0沿x轴分布图

例2－6　时间连续点源沿一维空间（x方向）扩散，将坐标原点O取在点源中心，单位时间投放的污染物质量为m且恒定不变，把连续时间τ看成许多时间单元dτ组成，时段dτ内投放的质量为mdτ，可以把时间连续源看做是无限多个mdτ所组成的瞬时点源的叠加。求时间连续点源一维扩散的解析解形式。

解：根据瞬时点源的解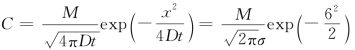，注意：上式中σ并非常数，而与时间t有关。对任意时刻t的浓度所要求的σ值等于，（t－τ）为时间间隔，τ为投放时刻，t为所求时刻。

当τ＝0时，，为瞬时点源；

当τ＝t时，σ＝0，未扩散。

在dτ时段内投放的质量dM＝mdτ，该质量在x断面引起的浓度变化为

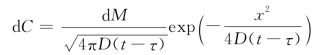
故

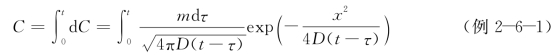
令，则

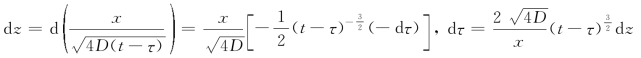
当τ＝t时，z＝∞；当τ＝0时，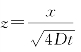

故式（例2－6－1）成为

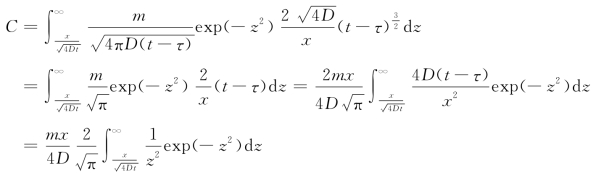
采用分部积分法

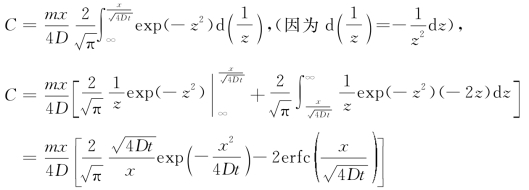
故。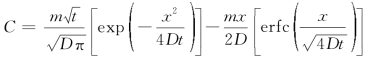

时间连续点源的污染范围和浓度均随时间增加而增大，如图所示。

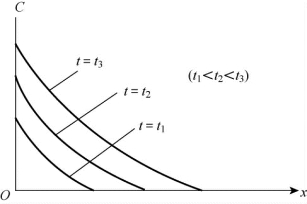
例2－6图