环境水力学：静止水体中瞬时点源扩散的二维和三维空间

将瞬时源投放于宽浅的河流或湖泊上，则污染物的扩散可由二维扩散方程＝描述，相当于无限长瞬时线源的扩散。

卡斯若（Carslaw）等人曾做过理论推导，认为在不同方向上的扩散没有相互影响。令xoy平面上任意点的浓度C（x，y，t），可由两部分浓度C1（x，t）和C2（y，t）的乘积构成，则C（x，y，t）＝C1（x，t）C2（y，t），

将其带入扩散方程，得到

整理得，

因C1＞0，C2＞0和浓度分布的对称性，必有

可以看出，C1（x，t）和C2（y，t）为各自满足静止水体中瞬时点源一维扩散方程的解，即

其中

M为瞬时投放的质量。俯视其浓度线为同心圆，源点处浓度最大，随着离源点的距离增加，浓度成负指数函数衰减。

演绎到三维空间，Fischer等人（1979）给出了下式：(www.xing528.com)

其中

例2－4　浓度分布式分别为下列两种情况下，求出最大浓度的表达式及最大浓度出现在什么位置。

（1）浓度分布式采用式（2－54）给出的三维瞬时点源公式；

（2）浓度分布式为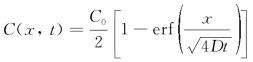（一维起始无限分布源扩散的浓度分布）。

解：

（1）最大浓度是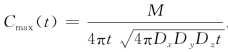：。最大浓度出现在指数等于0的点，因此Cmax（x，y，z）＝C（0，0，0）。

（2）误差函数的定义域是（－∞，＋∞），值的区间是［－1，1］。最大浓度出现在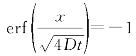的点上，而且Cmax（t）＝C0。当误差函数的参数趋向于－∞时出现最大浓度Cmax。在t＝0时，最大浓度出现在所有x＜0的点上；当t＞0时，最大浓度只出现在x＝－∞这一点上。