一、均值及方差
利用式(2-42)可以求解任意时刻沿x轴方向的浓度。不难看出,式(2-42)正是高斯分布的表达式。若以时间t为参数,画出浓度沿x轴的分布,如图2-4所示。由图可见,随着时间的增长,扩散范围变宽而峰值浓度变低,浓度分布曲线愈趋扁平。在t接近于零时,峰值浓度最大。
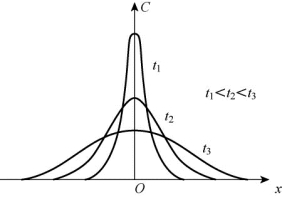
图2-4 静止水体中瞬时点源浓度沿x轴的分布图
若将浓度C看成随机变量,可求出关于C的各阶原点矩,表示为Mn(n为阶数)如下:
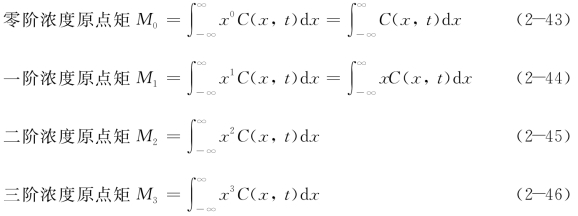
从上面的定义不难看出,零阶浓度矩是代表浓度分布曲线与x轴所包围的面积,也就是全部扩散物质的质量,因此对任何时刻零阶浓度矩M0保持为常数。令μ为浓度分布曲线的重心距x轴坐标原点的距离,则
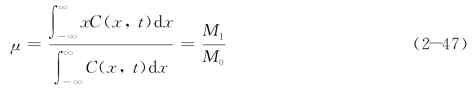
一阶浓度原点矩为随机变量C的数学期望(均值)。若将x轴坐标原点取在源平面处,此时一阶浓度原点矩为零,质量中心坐标μ=0,浓度分布曲线是以通过x=0的纵轴为对称轴。
令σ2为浓度分布的方差,则
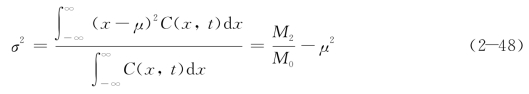
方差是衡量浓度分布曲线扩展宽度的一种尺度。σ2越小,表示曲线趋于集中在均值附近。把浓度分布函数式(2-42)代入式(2-48)并积分可求得方差σ2和标准差σ:
![]()
上式说明方差是随时间t的增加而增大,时间愈久,扩散宽度愈大。图2-5所示为不同标准差的浓度分布形态。
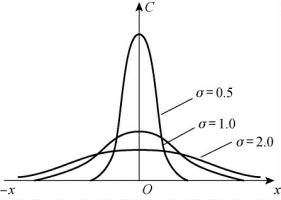
图2-5 静止水体中瞬时点源不同标准差的浓度分布图(https://www.xing528.com)
因浓度分布曲线的标准差随时间而变,若将式(2-49)对时间求偏导数得

若在一个不长的时间间隔内,以差分代替微分,得到

若已知不同时刻的浓度分布,应用上式即可计算分子扩散系数值。从理论上讲,浓度分布曲线x轴向两端应延伸至无穷远处,但可以证明,在以对称轴为中心的分布宽度为4σ的范围内,分布曲线与x轴所围的面积可以达到总面积的95%,如图2-6及表2-3所示。所以从实用观点考虑,可认为其分布宽度等于4σ,如果坐标原点与源平面重合,则曲线的分布区间可认为是(-2σ,2σ),若坐标原点与源平面不重合而相距μ,则曲线的分布区间可认为是(μ-2σ,μ+2σ)。
将标准差关系式(2-49)代入浓度公式(2-42),得到
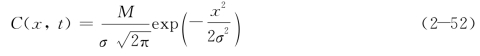
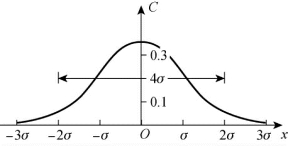
图2-6 静止水体中瞬时点源扩散解的方差分布
表2-3 静止水体中瞬时点源扩散解的方差分布

例2-3 对于一维瞬时扩散点源,比率C/Cmax可以写成参数α的公式,使它满足x=ασ。试运用该公式估算浓度曲线数据中的扩散系数D。
解:从前面的例子我们知道![]() ,因此我们可以将式(2-42)改写成
,因此我们可以将式(2-42)改写成
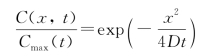
我们将![]() 和x=ασ代入上式得到
和x=ασ代入上式得到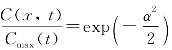 。这里α是一个参数,如取α=1.0,即x=σ,这时,
。这里α是一个参数,如取α=1.0,即x=σ,这时,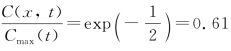 。在标准化后的浓度曲线上找到
。在标准化后的浓度曲线上找到![]() 的点并用他们度量σ值。然后我们可以根据
的点并用他们度量σ值。然后我们可以根据![]() 和t的值估算扩散系数D。
和t的值估算扩散系数D。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




