水力学中静止水体的一维扩散方程求解

图2－3　无限长管道中一维纯扩散示意图

现研究如图2－3所示的一水平放置直径较小的无限长水管，管中充满静止水体，在管子中间断面瞬时（t＝0时）投放有色溶液，在投放平面上有色溶液的浓度均匀分布，设有色溶液的比重和水一样。令投放平面和坐标原点重合，横坐标轴x与管轴线平行如图所示。由于管壁的限制，有色溶液只能沿管轴方向作一维扩散，虽然有色溶液分布在横断面的平面上，但它所代表的问题的性质和点源的一维扩散相同。沿着y轴和z轴方向上的浓度梯度为零，上述是一个非恒定的一维扩散问题，式（2－9）即为问题的方程表达形式。

观察式（2－9），可以得到三个要点：

（1）式中时间变量为一阶，因而要想求得解，必须指定一个初始条件，得到解是一个非恒定的、随时间变化的值。若要求得不随时间变化的恒定解，必须设，就无需另设初始条件。有恒定解形式的称为拉普拉斯方程。

（2）式中距离变量为二阶，因而要想求得方程的解，必须设定两个边界条件，所得到的解因距离而变化。

（3）式子的形式与热传导方程几乎完全相同，唯一的不同点是扩散方程的系数为扩散系数D，而热传导方程的系数为热传导系数k。

要解此方程，需要两个边界条件和一个初始条件。对于边界条件，由于示踪分子不可能扩散到无穷远处，所以浓度在x＝±∞时始终为0。

初始条件设定为：将染料示踪剂均匀的注入一个垂直于x轴的截面之上，截面宽度无穷小。应用狄拉克δ函数表示，初始条件为：

式中狄拉克函数δ（x）在除x＝0外处处为0，但是δ（x）的在（－∞，＋∞）上的积分值为1。因而扩散物质的投加量表达式为：

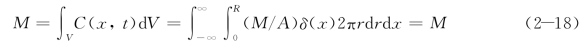
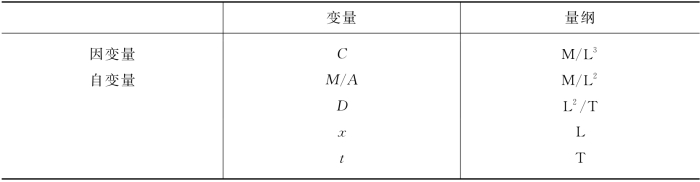
应用量纲分析法，需要考虑到解的所有控制参数。因为任意时刻在x方向某一点的浓度C必定与投放质量M、扩散系数D以及坐标位置x、时间t有关，表2－2总结了假定模型问题中涉及的因变量和自变量。从表中可以得到5个控制变量和3个量纲。由此可以构造两个无量纲量：

量纲分析可以得到π1＝f（π2），继而可以推导到浓度C的解为：

表2－2　管内一维扩散的量纲分析

可以通过两种基本方法找到函数f的表达形式。其一是通过多次实验测得数据，而后以π1和π2为横纵坐标绘出一条平滑曲线，即为函数f的曲线；其二是将式（2－21）作为微分方程的解，并求出f的解析解。此处对第二种方法进行陈述。

取新变量，则

应用链式法则计算，如下：

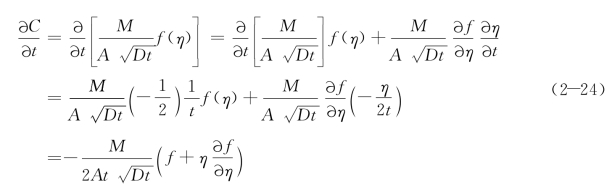
同理计算可得：

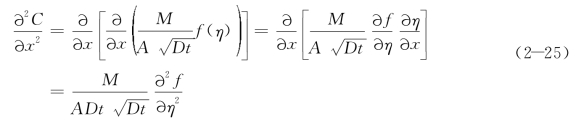
将上述式（2－24）、式（2－25）的结果代入扩散方程，可以得到一个以变量η表示的常微分方程：

要求解方程（2－26），需将边界条件和初始条件转化为f的两个新约束，因而将η代入边界条件可得

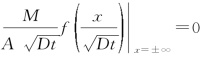C＝0，即，得到

我们使用相同的方式转化初始条件C（x，0）＝（M／A）δ（x），代换η得到：

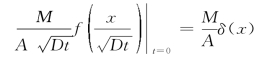
化简，得

(https://www.xing528.com)

式（2－28）中，方程左边如果x＞0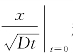，趋向于＋∞；如果x＜0，趋向于－∞，方程右边在t＝0时始终等于0，因此，初始条件可以简化为

因此，原来的偏微分方程中的三个条件（两个边界条件和一个初始条件）转化成了常微分方程中f的两个边界条件（2－27）或（2－29）。

另外一个要求是确定M值，从总量守恒得到

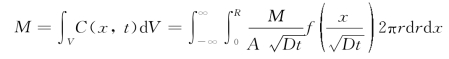
将代入并简化，得到：

首先我们利用恒等式

则式（2－26）式成为

积分一次得到

可以证明为了满足边界条件选择C0＝0是必需的（更多细节详见附录2－2）。

有了C0＝0这个条件，常微分方程的解可以很容易得到。由式（2－33）可以得到

方程两边移项整理可得

左右积分得

可以写成指数形式

由（2－30）有：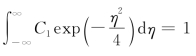

引入得到

进行坐标代换并且解C1可得：

查阅积分表可得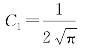

因此：

代换式（2－21）中的f得到：

这是环境流体力学中的经典结论，也是会贯穿整本书的方程式。