RADIOSS理论基础与工程应用：SPH方法的局限与解决方案

SPH方法是一种无网格纯拉格朗日方法，它最初由Gingold和Monaghan（1977年）和Lucy（1977年）用于天体物理问题中流体质团无边界三维空间任意流动问题的研究，如两星相撞、超新星爆炸以及月球形成等。经过多年的发展，它已应用在许多领域的研究，如天体物理学、弹道学、火山学、海洋学等。其理论基础来源于粒子方法，是把连续的物理量用一系列质点的集合的插值来进行数值解析，其核心是核函数，可以理解为在一定光滑长度范围内其他临近粒子对当前粒子影响程度的权函数。目前SPH方法只能用于3D分析类型。

由于是无网格算法，SPH方法要求SPH粒子的初始质量和坐标满足一定条件：所有SPH粒子应具有相同的质量，即相同材料的粒子（具有相同的初始密度）具有相同的体积。为实现这一规则，SPH粒子应分布在均匀的网格上（即均匀排列），其典型形式有两种：六角紧凑型和立方网格型。

六角紧凑型粒子分布如图20-1所示。

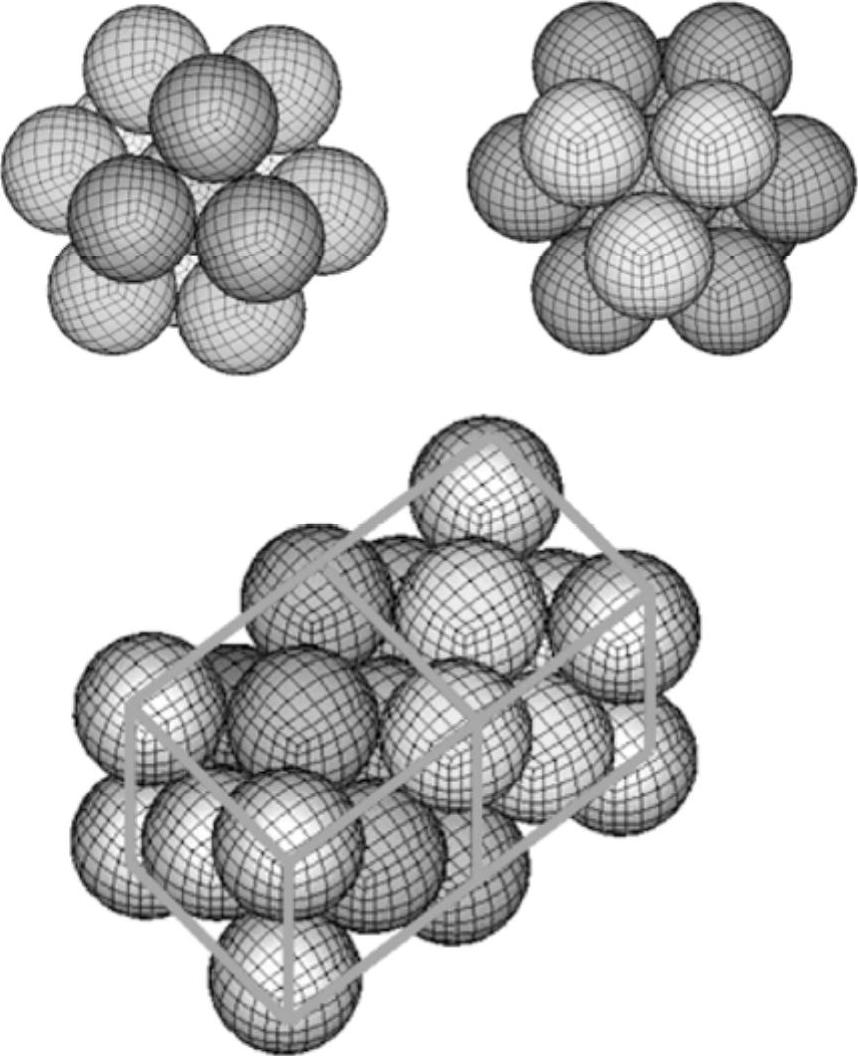
图20-1 六角紧凑型粒子分布

其中，光滑长度h₀表示了六角形紧凑分布形式下任意一粒子与其距离最近的粒子的距离。每个粒子的质量m_p在该PART使用的粒子属性（/PROP/SPH）里定义，与材料密度和标称长度有关：

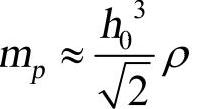
由于整个被SPH粒子填充的空间可以看做是与粒子数量相等的正多面体空间，则每一个粒子在所占据的体积可以表示为：

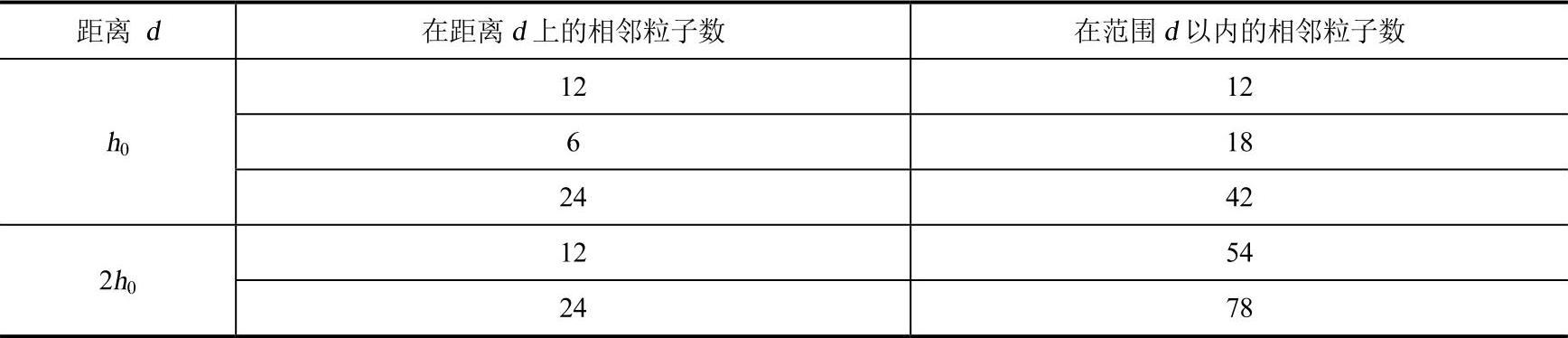
核函数加权在超过距离2h（h为光顺距离）后不起作用。在六角紧凑型SPH粒子排布中，若其光顺距离为h₀，则在距离2h₀的范围内，每一粒子均有54个邻粒子，如表20-1所示。

表20-1 六角紧凑型分布相邻粒子数与光顺距离的关系

如果启动了SPH校正功能，需要注意的是，即使是光顺距离h的轻微增加，也会导致整个SPH模型在拉伸行为时的数值出现不稳定现象。因此，如果在模型中采用了六角紧凑型粒子排布方式，并使用了SPH校正功能，那么我们建议用户将光顺距离h设置为小于最小的任意两个粒子之间的距离，且物理模型中无拉伸现象发生。在模型受到拉伸的作用时，光顺距离h的设置可以大于这个值，以限制SPH方法的数值不稳定现象的发生，但更大的光顺距离意味着更大的计算消耗。

对于立方网格型分布，假定在边长为c的立方体中有一个粒子，则粒子的质量m_p与材料的密度及立方体长度c之间有如下关系：(www.xing528.com)

表20-2是立方网格型分布时，在距离d范围内的相邻粒子数。

表20-2 立方网格型分布相邻粒子数与距离的关系

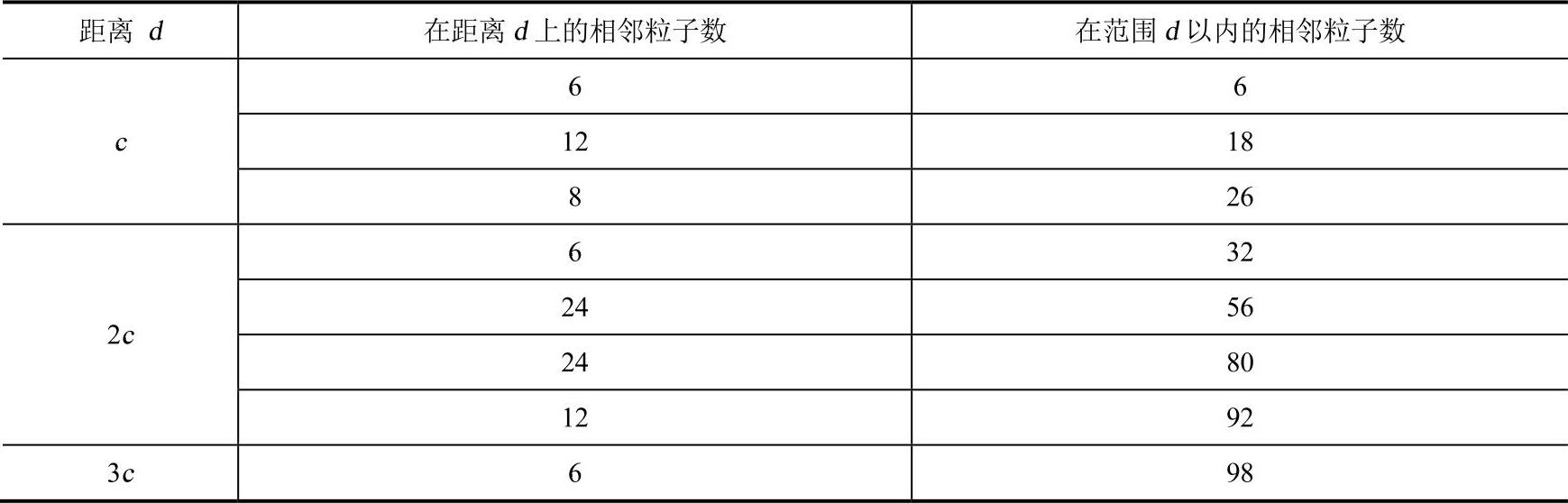
为解决拉伸行为的不稳定性，根据经验，相对于六角紧凑型分布方式，立方网格型分布时需要考虑更多的相邻粒子数，光滑长度在1.25c～1.5c是比较好的设置。如果将光滑长度h取为1.5c，则每个粒子在2h距离内将有98个相邻粒子，而对于六角紧凑型分布，在2h距离内只有54个相邻粒子（见表20-1）。

在实际使用SPH建模时，除SPH粒子必须均匀分布外，需要特别注意的是，所建立模型代表的实际尺寸，如图20-2所示。

HyperMesh对于SPH离散的设置：

● 立方网格型，以8为小组布置SPH粒子，每个粒子位于一个立方体的角点。

● 六角紧凑型，以14为小组布置SPH粒子，生成在立方体的8个角点和六面的中心。这类似于六方密排晶格结构，并被推荐应用到RADIOSS模型中。

这也决定了SPH粒子之间的距离，因此较小的值将导致更多的单元在同一空间，但这不会影响表现粒子实质的质量或密度。

在定义SPH粒子与结构网格的相互作用时，比如Interface Type 2和Type 7时，SPH粒子必须作为slave 一侧，而分属不同PART的SPH粒子之间则不需要定义任何接触设置。

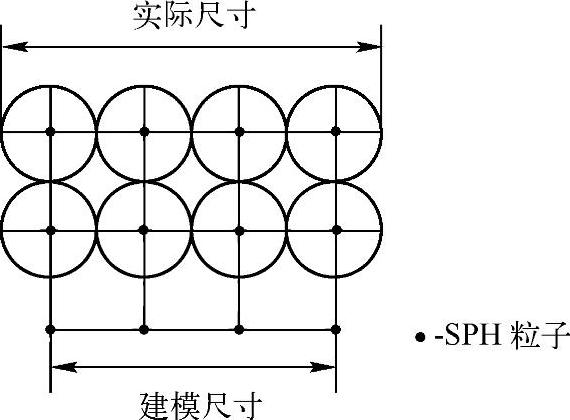
图20-2 SPH建立模型代表的实际尺寸