对于结构常用的金属及其合金材料,如各种钢材、铝合金等,工程建模分析中一般采用基于连续性假设的弹塑性材料模型。RADIOSS Block里有如表16-27所示的材料模型可以用来描述金属合金。
表16-27 RADIOSS Block里的材料模型
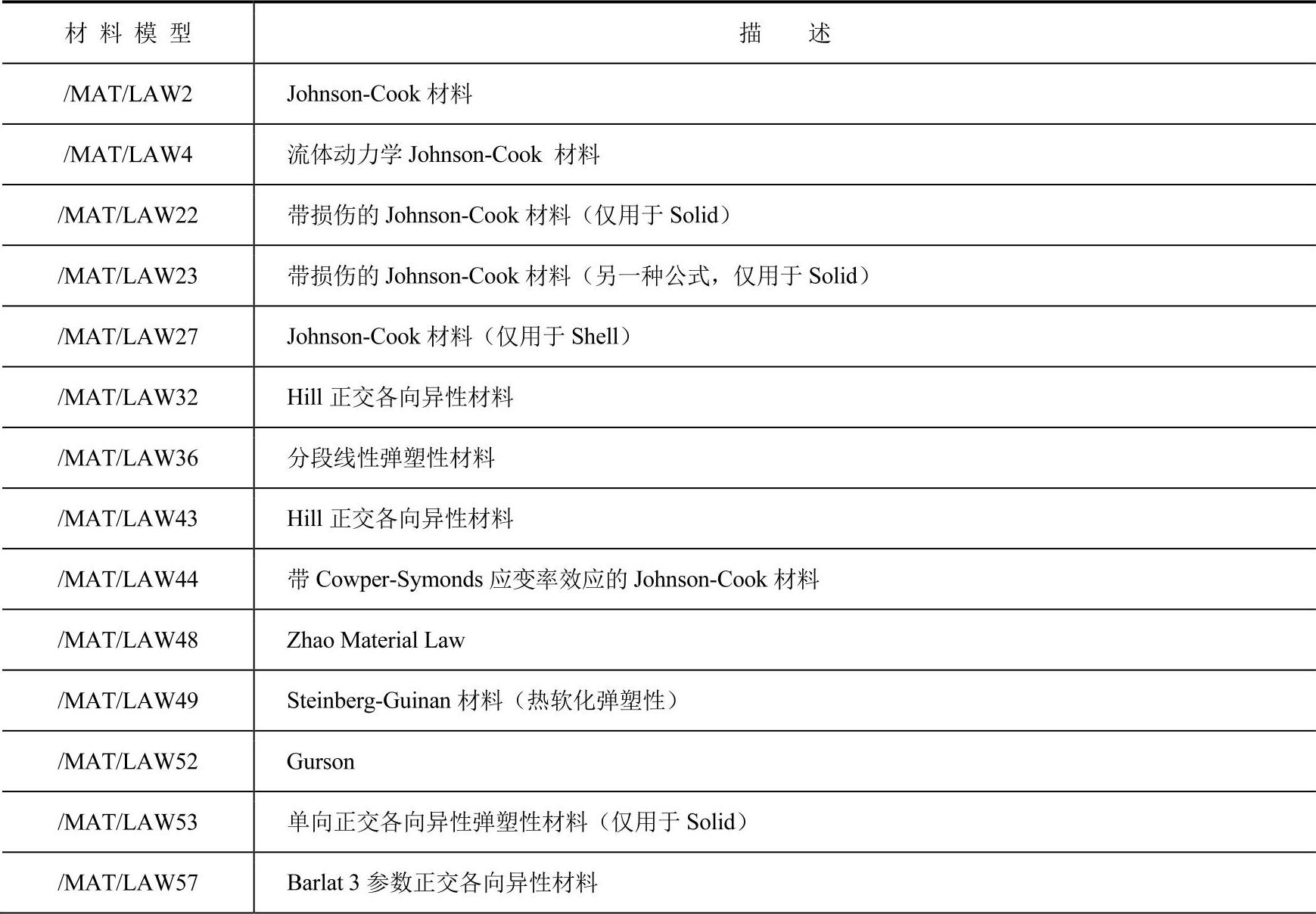
(续)

1.标准拉伸试验数据到FEA输入数据的转换
为了获取材料的力学性能参数,最常见的测试方法是进行拉伸试验,获得图16-9中曲线A所示的工程应力-应变曲线,并依此得到屈服强度、抗拉强度、伸长率等参数。

图16-9 应力-应变曲线
其中工程应力与工程应变定义如下:
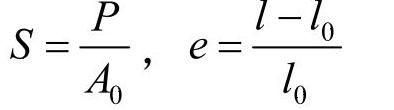
式中,P是载荷;A0是试样的原始横截面积;l0是试样的原始标距长度;l是试样变形后的长度。
上述应力-应变曲线中的工程应力、应变是以试样的初始尺寸进行计算的,事实上,在拉伸过程中试样的尺寸是在不断变化的,尤其是超过材料的屈服强度后,试样的尺寸相对于原始值已有了较大的改变。为了表达材料真实的应力状态,工程上使用考虑瞬时载荷和瞬时截面积的真实应力来度量材料的真实应力状态,而其对应的应变称为真实应变(或对数应变)。
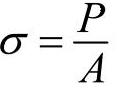
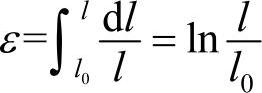
式中,P是瞬时载荷;A是试样的瞬时截面积;l0是试验的原始标距长度;l是试样的瞬时长度。
由塑性流动过程中体积不变的条件,易得到工程应力、应变与真实应力、应变的换算关系为

这样工程应力-应变曲线可以转换成真实应力-真实应变曲线,如图16-9中曲线B所示。
另外,在有限元分析中,描述材料的流动行为时通常会用到塑性应变这个概念,塑性应变等于真实总应变减去弹性应变,其计算公式如下:
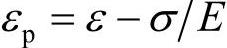
有限元分析中常用的弹塑性材料模型都是对材料的真实应力与塑性应变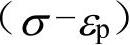 关系进行的数学描述,因此,需要首先将从材料供应商处获得的工程应力-应变曲线按上式进行转换,然后按照选用的材料模型对其进行表达。
关系进行的数学描述,因此,需要首先将从材料供应商处获得的工程应力-应变曲线按上式进行转换,然后按照选用的材料模型对其进行表达。
对于LAW36,不涉及数学表达式的构建,各应变率下输入的曲线即为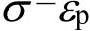 曲线。而对于LAW 2及LAW27材料模型,则需要对Johnson-Cook模型的参数进行反求。其步骤如下:(https://www.xing528.com)
曲线。而对于LAW 2及LAW27材料模型,则需要对Johnson-Cook模型的参数进行反求。其步骤如下:(https://www.xing528.com)
得到真实应力-真实应变曲线(如上所述)。
确定参数a,将0.2%应变对应的真实应力作为参数a,如图16-10a所示。
得到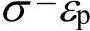 曲线(如上所述),如图16-10b所示。
曲线(如上所述),如图16-10b所示。
数学变换得到曲线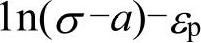 ,如图16-10c所示,并对数据点使用直线拟合,纵轴截距即为参数b,斜率为参数n。(注:也可对真实应力-塑性应变曲线进行曲线拟合,反求参数b和n,详见Hyper Math相关帮助文档和例子)。
,如图16-10c所示,并对数据点使用直线拟合,纵轴截距即为参数b,斜率为参数n。(注:也可对真实应力-塑性应变曲线进行曲线拟合,反求参数b和n,详见Hyper Math相关帮助文档和例子)。
在真实应力-真实应变曲线上取得参数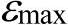 ,如图16-10d所示。
,如图16-10d所示。
在真实应力-真实应变曲线上计算得到参数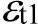 和
和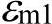 ,如图16-10d所示。
,如图16-10d所示。
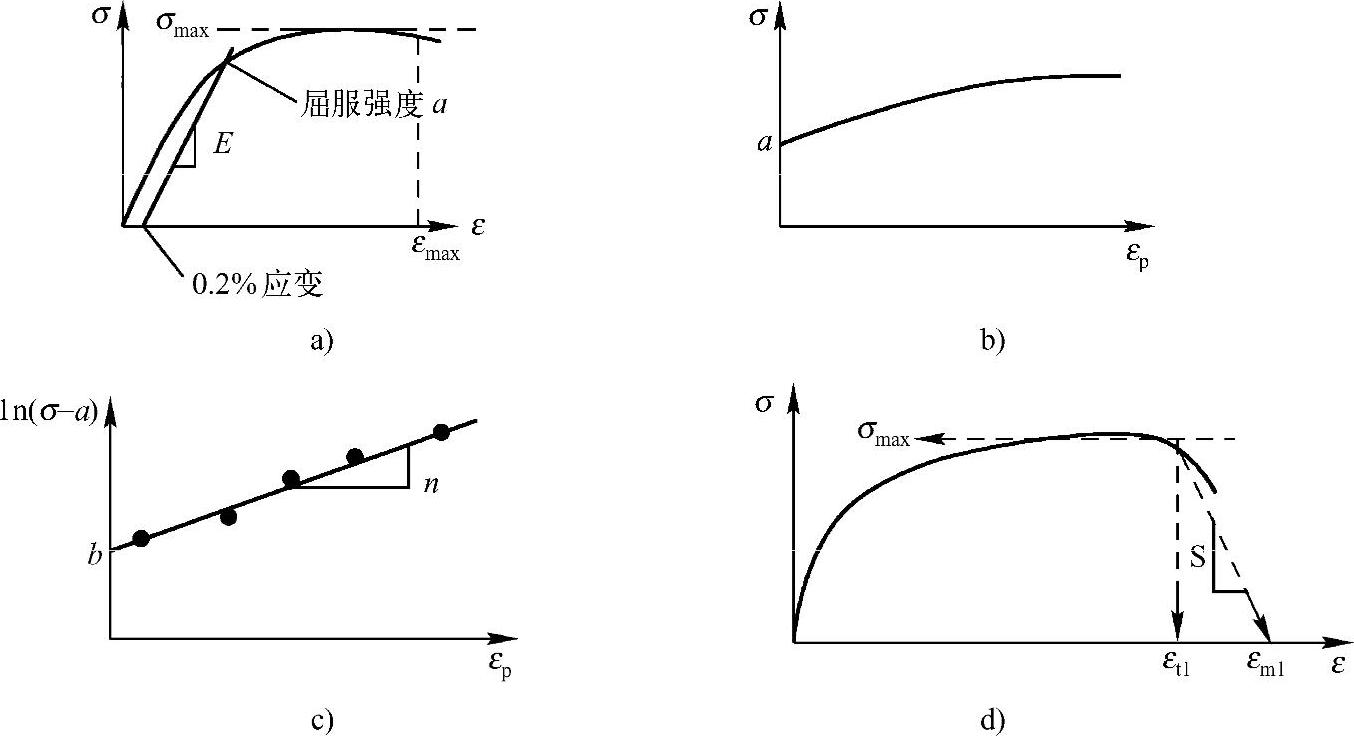
图16-10 确定LAW2的参数
2.金属失效模拟
对于常见的金属及其合金材料,理论上,只要失效模型、单元类型、材料模型三者同时兼容,则失效模型就可以用于模拟该材料的失效。但在实际应用中还应考虑分析对象的实际载荷状态,比如对于受压缩载荷失效的分析对象,只定义拉伸失效模型是没有实际意义的。对于带有分层失效的复合材料分析对象,仅使用/FAIL/CHANG失效模型也是不充分的,而使用/FAIL/HASHIN则更为合适。也就是说,定义的失效模型应该至少包含分析对象主要工作载荷状态和失效载荷形态。
由于Johnson-Cook失效模型包含了全面的应力状态,包含压力相关性、应变率相关性和温度相关性,同时能与2D和3D单元兼容,因而适用范围非常广泛。
其失效应变表达式为
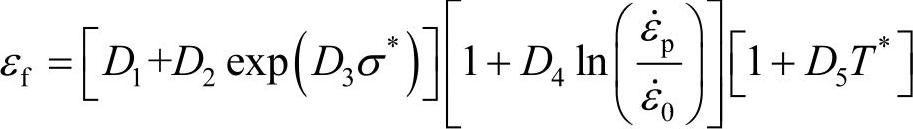
在某些特定的应力状态下,应力三轴比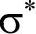 可以直接使用解析值,这为该失效模型参数
可以直接使用解析值,这为该失效模型参数
Di(i=1,…,5)的试验确定提供了工程上的方便性。比如,在纯拉伸状态下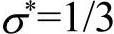 ,在纯剪切状态下,
,在纯剪切状态下,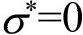 ,在纯压缩状态下,
,在纯压缩状态下,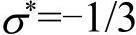 。如果忽略应变率项D4和温度项D5,则由上述三种试验准静态测试的失效塑性应变可求解参数D1、D2、D3。现举例说明如下。
。如果忽略应变率项D4和温度项D5,则由上述三种试验准静态测试的失效塑性应变可求解参数D1、D2、D3。现举例说明如下。
假定某材料在纯拉伸试验测试得到的失效塑性应变为0.4,纯剪切试验的失效塑性应变为0.564,纯压缩试验的失效塑性应变为0.830,忽略D4和D5(均设为0)。则可列方程如下:
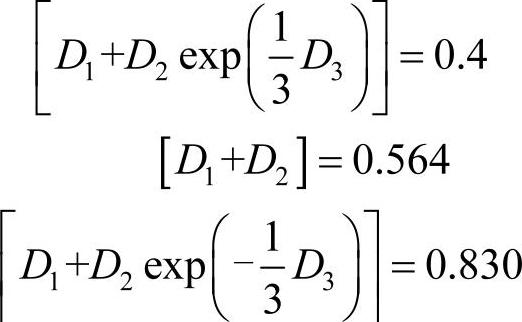
可求得D1=0.246,D2=0.3,D3=-2。则该材料的失效塑性应变-应力三轴比曲线的形式如图16-11所示。
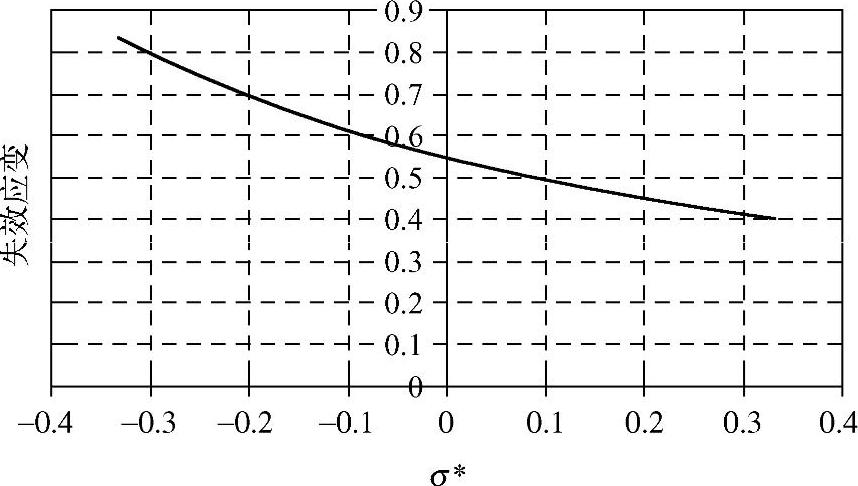
图16-11 材料的失效塑性应变-应力三轴比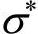 曲线
曲线
如果有条件,增加每种试验的动态测试,则可将应变率效应包含进去,得到参数D4。对于参数D5,则需要增加温度软化相关测试。
同时,由上例可以看出,与单一的拉伸失效模型相比,Johnson-Cook失效模型使用应力三轴比以包含更全面的应力状态,使其适用范围更广,这也是该失效模型广泛应用的原因之一。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




