Shell(板壳)单元由中面网格和厚度属性定义,基于厚度远小于其他两个维度的假设,如图15-10所示。Shell单元是最常用的单元,例如在汽车碰撞模型中,90%以上的单元都是Shell单元,它们包含膜、弯曲和剪切变形,厚度方向正应力始终是0。
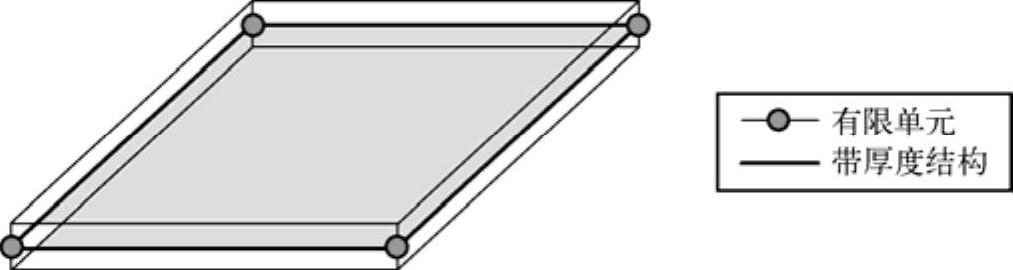
图15-10 Shell单元定义
RADIOSS里标准的Shell单元是带横向剪切变形的Mindlin板单元,这种单元比标准的 Kirchhoff单元精确,后者不考虑横向剪切变形,以至于初始垂直于中面的几何横截面在变形后依然垂直于中面。
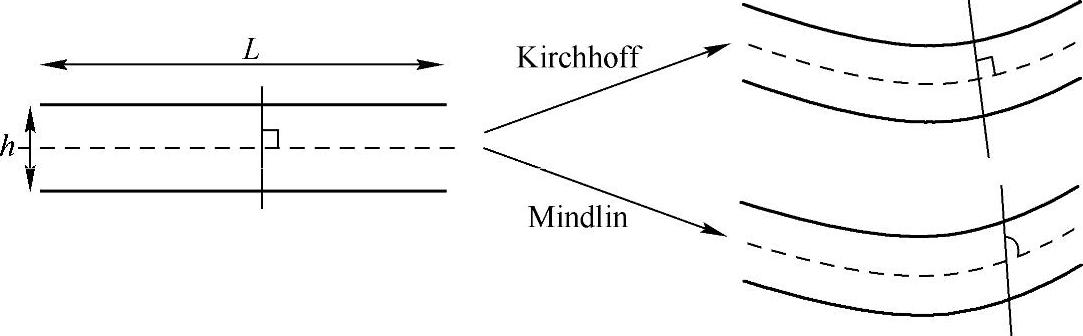
图15-11 Shell理论假设
尽管Kirchhoff模型精度稍低,如果L/h>20,kirchhoff假设还是正确的。但是如果L/h在10~20时,这种初始垂直于中面的横截面依然垂直于中面的假设就不再成立。而Mindlin板始终考虑横向剪切,不存在理论假设不成立的问题。RADIOSS Block里减缩积分Shell单元(无论3节点还是四节点)都是基于Mindlin假设,没有特别的公式用于解决单元节点偏离几何中面的情况,因此对于薄壁结构的网格离散,使用中面划分网格是非常重要的。
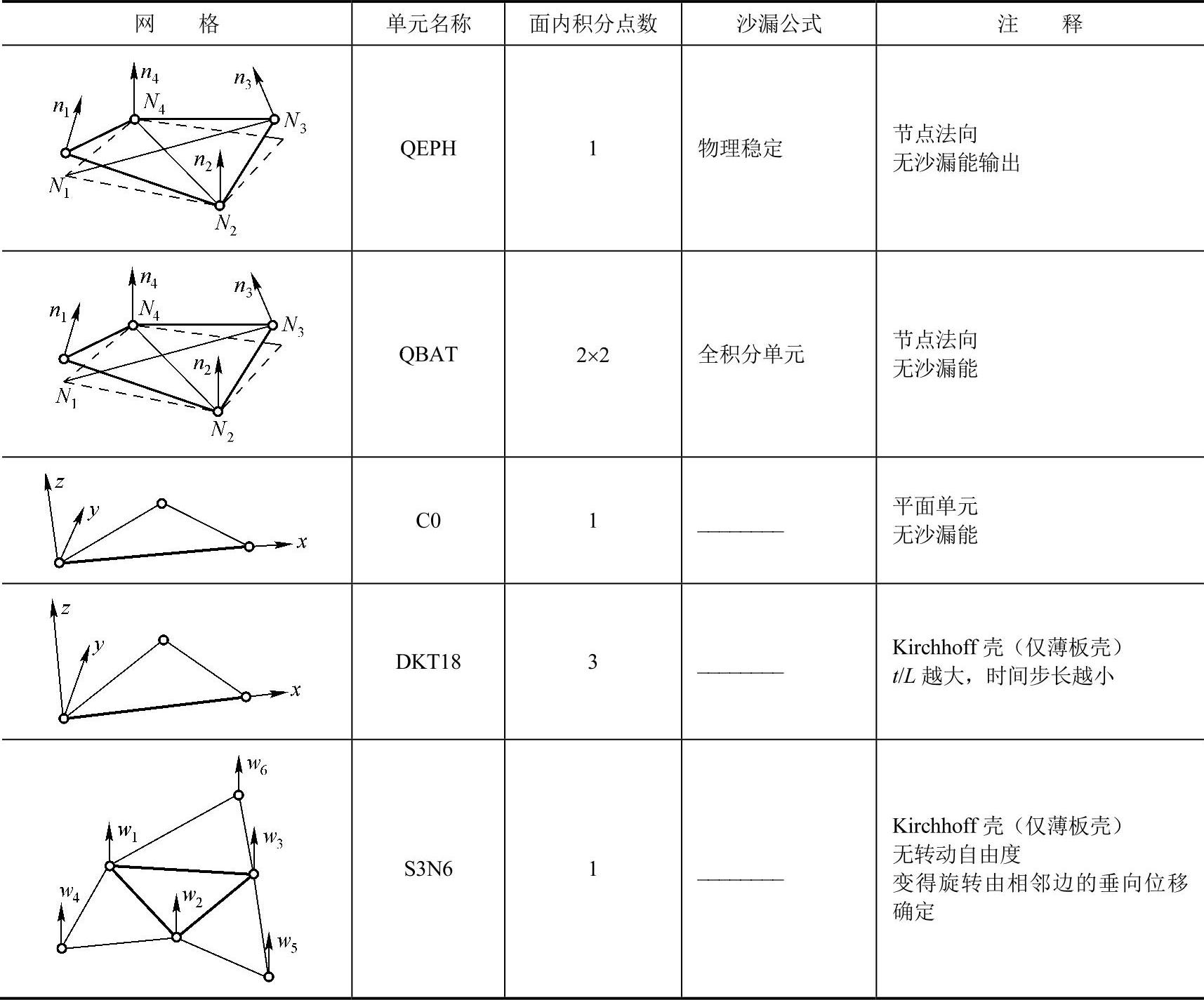
在碰撞分析中,Shell单元公式是一个很重要的要素。RADIOSS的Shell单元都是基于Mindlin-Ressner板壳理论。这种公式不但对薄板壳有效,对与厚板壳也基本适用。RADIOSS不但有因为计算效率而最流行的减缩积分Shell单元,还有完全积分的四边形壳单元(QBAT)和三角形单元(DKT18)。表15-11给出了各种壳单元的概况。
表15-11 RADIOSS Shell单元概要

(续)
对于给定的应用领域,如何选择Shell的单元公式需要一定的经验,下面是选择Shell单元公式的可能有用的基本概念:
(1)BT单元简单、高效、计算开销小。作为减缩积分单元,这种单元对网格质量不是太敏感,可以用于较粗糙的网格。
(2)对于准静态分析、精细网格、翘曲表面、屈曲,这些情况选择QEPH或者QBAT是明智的。
(3)QBAT是RADIOSS里精度最高的Shell单元公式,但是由于它是完全积分,其计算开销是BT单元的2~3倍。
(4)QEPH是精度和计算开销协调最好的Shell单元,它相对BT单元增加的计算开销不大于15%,而其得到的结果接近于完全积分的QBAT单元。(https://www.xing528.com)
(5)不建议使用三角形单元。C0单元太刚硬,而DKT18计算消耗很高。为了保证结果的质量,一般应限制三角形单元比例不超过5%。
(6)S3N6单元在弯曲行为精度同DKT18,可以应用在一些特殊的领域,比如冲压仿真。
求解精度与网格的基本关系如图15-12所示。
对于弹性Shell,正应力沿厚度方向是线性分布的,因此单元内能可以使用解析积分方法获得。在塑性情况下,这个应力分布是非线性的,并且至少需要在厚度方向3个积分点才可以将这种非线性考虑进去。这种非线性的应力分布需要增加积分点数才能够计量,同时单元内能的估算的精度依赖于积分点数。因此需要在考虑材料非线性、料厚和弯曲速率的前提下调和计算开销与解的精度关系。厚度方向使用过5个积分点能够给出较好的结果,尤其对于厚度超过2mm的板,当然这样带来的CPU开销的增加也是不能忽略的。仿真无弯曲和横剪的膜单元时,厚度方向使用1个积分点就够了。当然,对于线弹性材料(Law1),由于是可解析的,厚度方向积分点数可以忽略。
另一个低CPU开销而结果相当精确的做法是使用全局积分。这种积分方式把Mises塑性准则转化为成Illuyshin准则,这样积分点处的应力分量被内力(N,M,T…)取代。
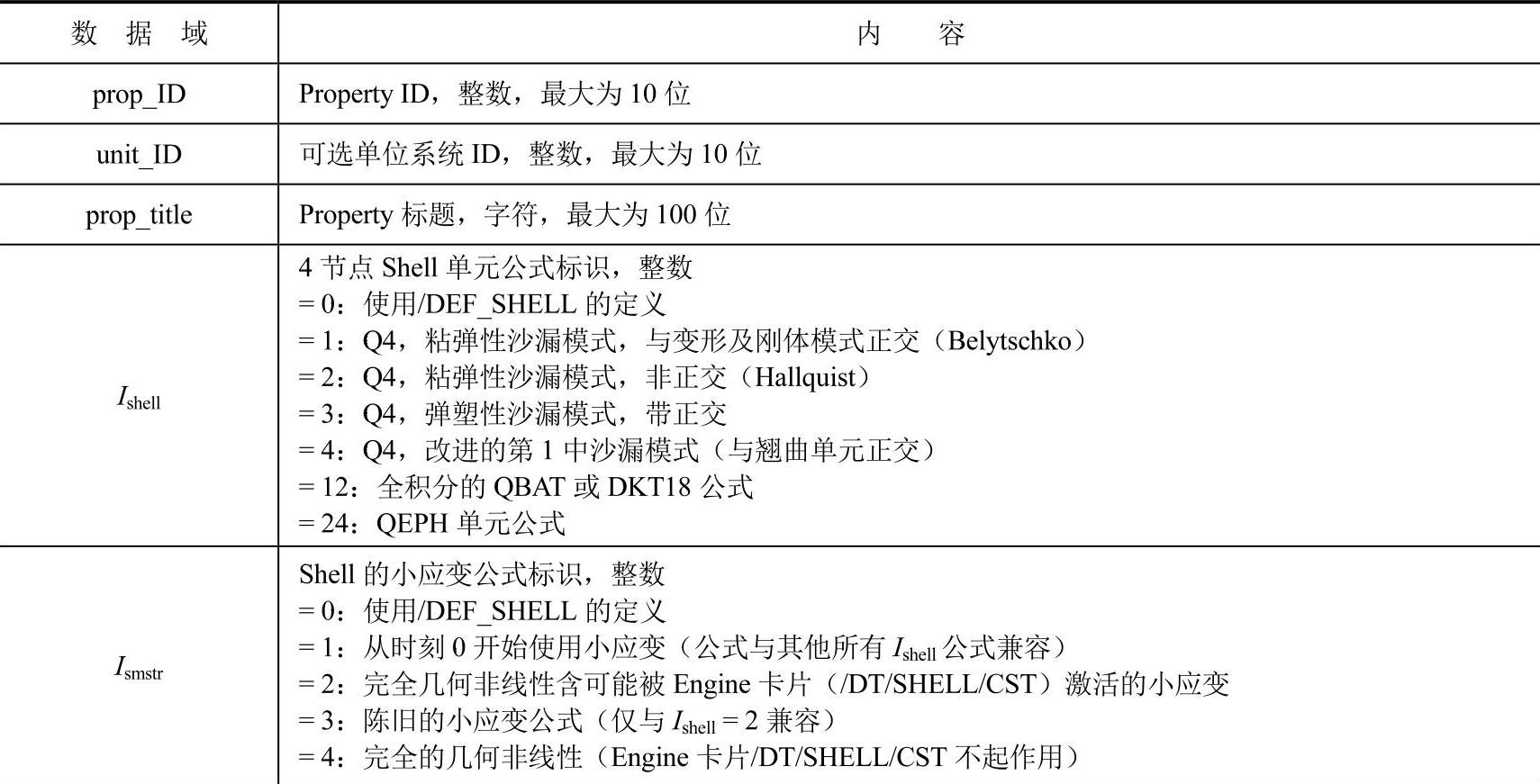
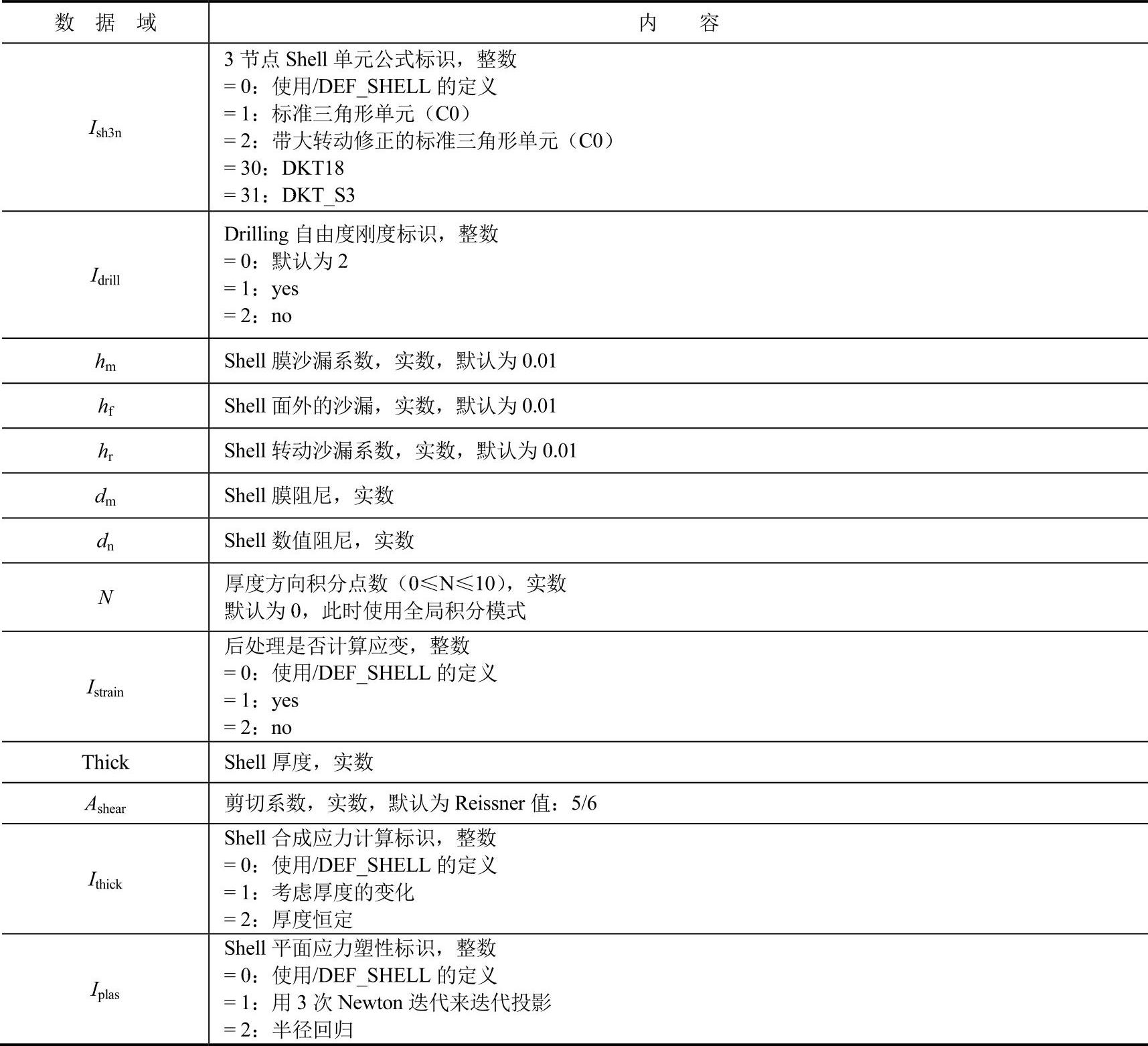
Shell单元的属性卡片格式如表15-12所示。
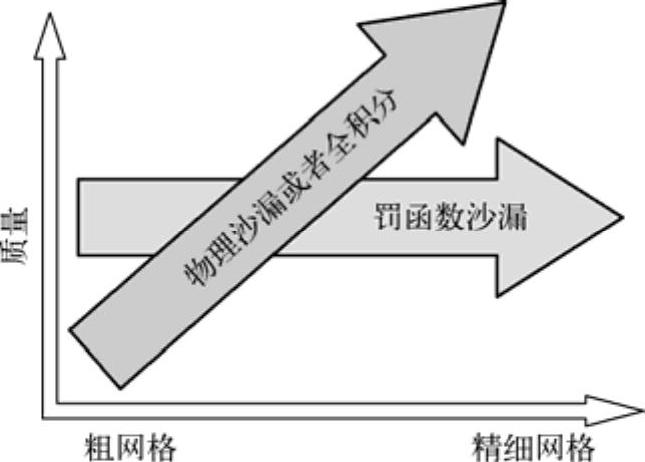
图15-12 Shell单元在不同网格里的应用
表15-12 Shell单元的属性卡片

各参数的解释如表15-13所示。
表15-13 Shell单元的属性参数说明
(续)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




