RADIOSS梁单元（Beam）的理论基础与应用

RADIOSS Block里有两类Beam单元，分别是欧拉-伯努力梁（Euler-Bernouilli）和基于铁摩辛柯（Timoshenko）理论的积分梁，分别对应/PROP/BEAM或/PROP/TYPE3，和/PROP/INT_BEAM或/PROP/TYPE18，我们将其分别记为Beam和Int_Beam。

1.经典梁（Beam）

Beam只能与线弹性材料模型（/MAT/LAW1）和弹塑性Johnson-cook材料模型（/MAT/ LAW2）匹配使用。Beam的定义需要3个节点，其中N3用于描述或确定梁截面在空间的方向，即按右手定N1-N2-N3所确定的方向是梁截面高度方向（Beam的自身Z向）。因此，在建立Beam单元时，N3不能与N1-N2共线。

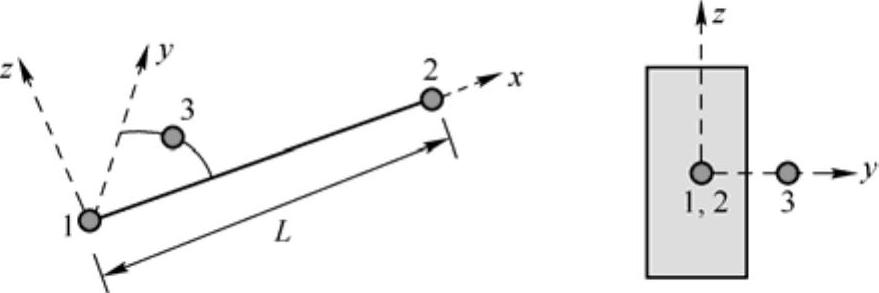
图15-2 Beam单元的定义

Beam单元的特征长度计算较为复杂，如式（15-3）所示：

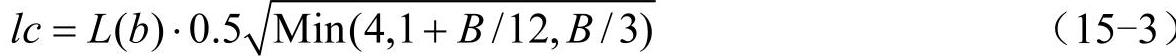
其中，L(b)是Beam单元的当前长度。

A是截面面积，Iy和Iz分别是自身Y向和Z向的截面惯性矩。

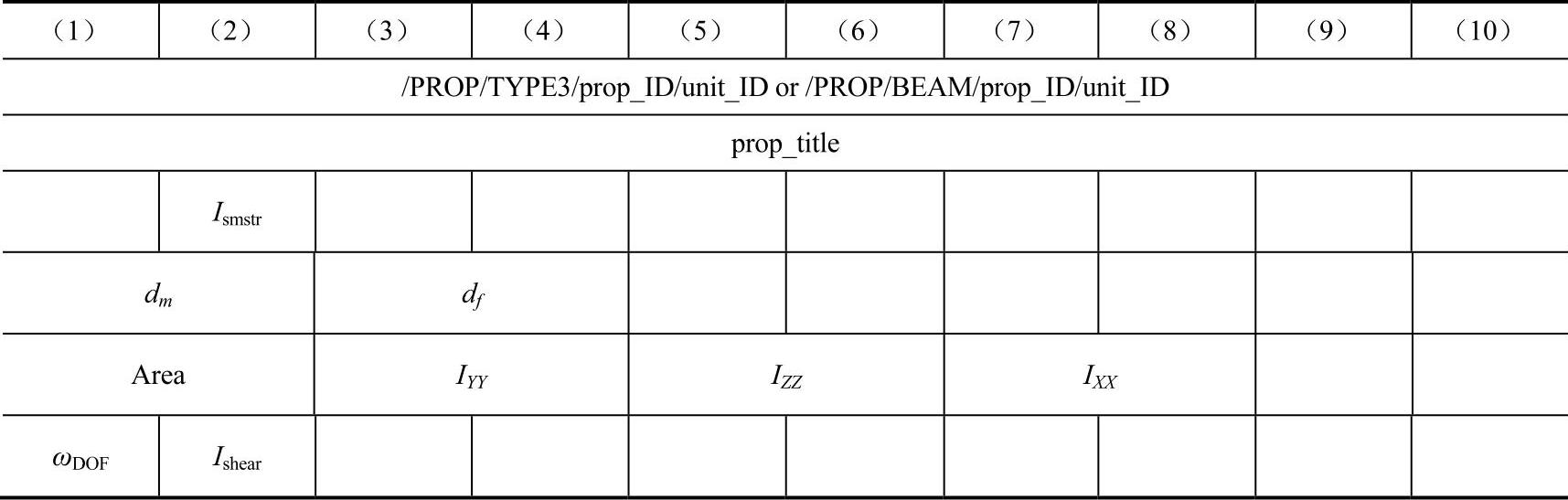
Beam的属性卡片格式如表15-3所示。

表15-3 Beam的属性卡片

各个参数解释如表15-4所示。

表15-4 Beam的属性参数说明

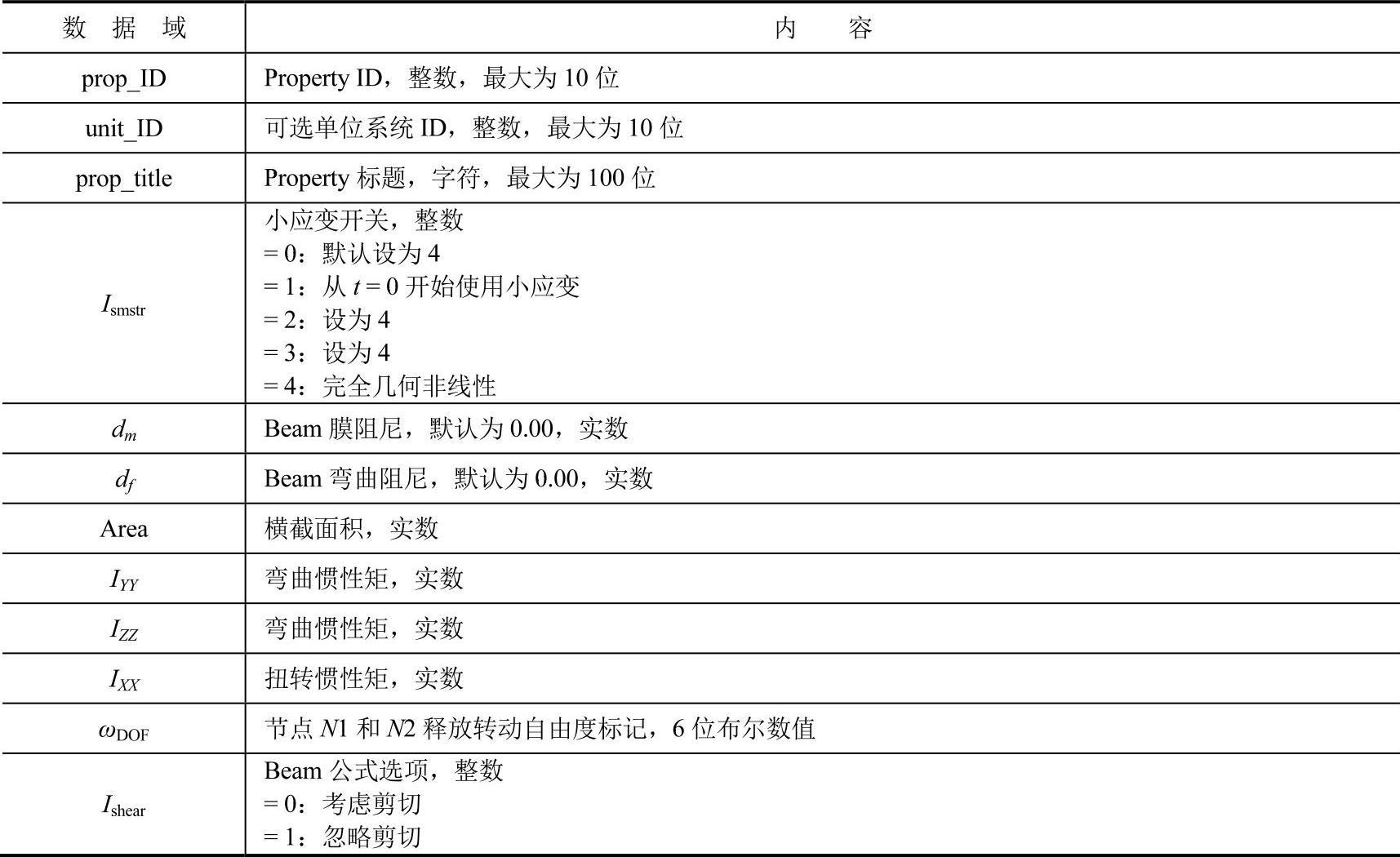
（1）如果I_smstr=1，则小应变从t=0时刻开始激活。这将使得Beam的分析加快，因为此时其临界步长是恒定的，但是小应变算法将使得Beam的精度不能严格保证。

（2）如果I_smstr=1，给定材料的应力应变数据是工程应力应变数据。否则，它们应该是真实应力应变数据。

（3）输入的参数用于确定3个截面惯性矩和截面积。为了保证精确性和稳定性，不建议输入无真实物理意义的参数，相关参数应满足如图15-3所示的基本关系。

2.积分梁（Int_Beam）(www.xing528.com)

Int_Beam是基于铁摩辛柯（Timoshenko）理论的积分梁，考虑横向剪切应变，但是不考虑扭转翘曲刚度，适用于截面大长高比（短梁）的情况。除了线弹性材料模型（/MAT/LAW1）和弹塑性Johnson-cook材料模型（/MAT/LAW2），Int_Beam还能与弹塑性分段线性材料模型（/MAT/LAW36）匹配使用。

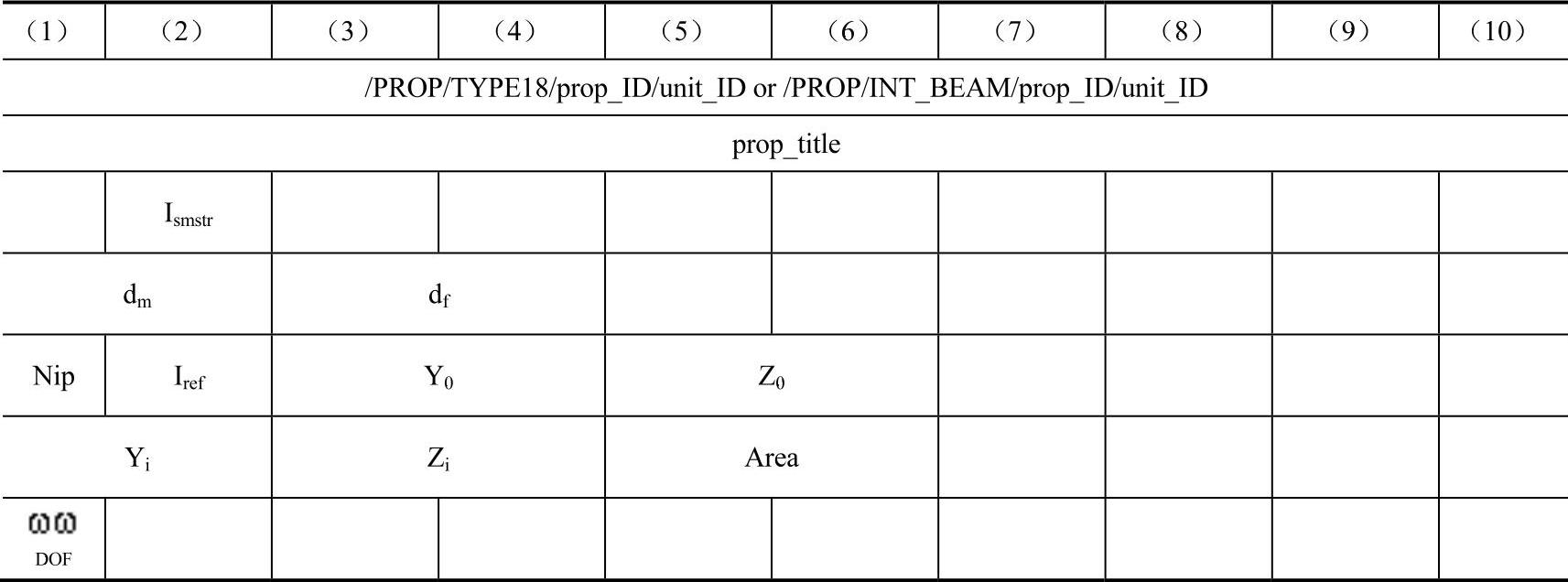
Int_Beam的属性卡片格式如表15-5所示。

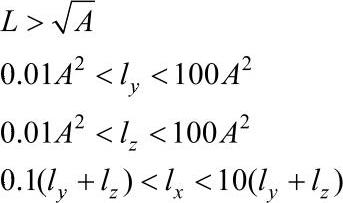
图15-3 Beam参数关系

表15-5 Int_Beam的属性卡片

各个参数解释如表15-6所示。

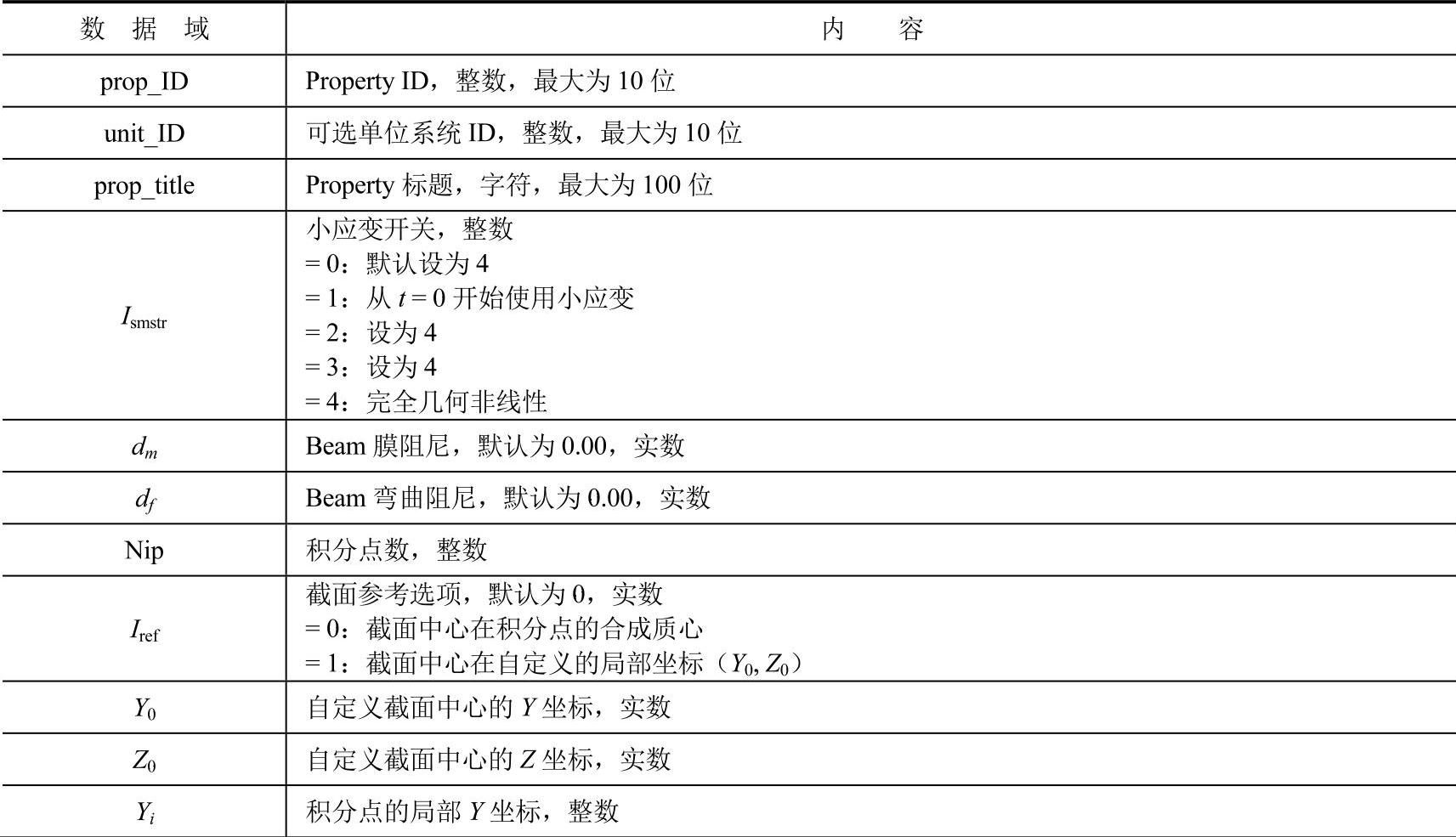
表15-6 Int_Beam的属性参数说明

（续）

（1）如果I_smstr=1，则小应变从t=0时刻开始激活。这将使得Beam的分析加快，因为此时其临界步长是恒定的，但是小应变算法将使得Beam的精度不能严格保证。

（2）如果I_smstr=1，给定材料的应力应变数据是工程应力应变数据。否则，它们应该是实应力应变数据。

（3）横截面最多可以定义100个积分点，如图15-4所示，截面单元的属性，如惯性矩和面积，按式（15-5）计算：

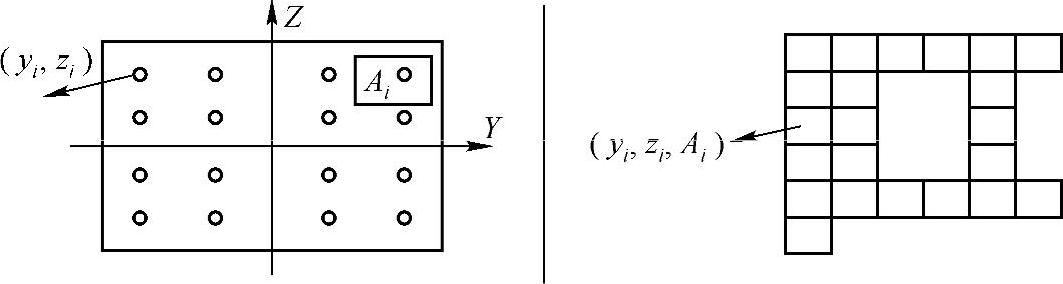
图15-4 Int_Beam的截面

积分梁通常用于模拟高横截面长高比（短梁）情况，使用多个积分点以允许在每个积分点处考虑基于von Mises准则的弹塑性。但是由于在长度方向仅有一个积分点，不推荐对框架结构的每根线上仅使用一个Int_Beam来考虑长度上的塑性过程，在截面高度方向也是这样。