RADIOSS非线性动力学有限元求解流程

基于上述控制方程的求解过程，结合有限元法的基本过程，可将非线性动力学的有限元求解过程概括如图14-2所示。

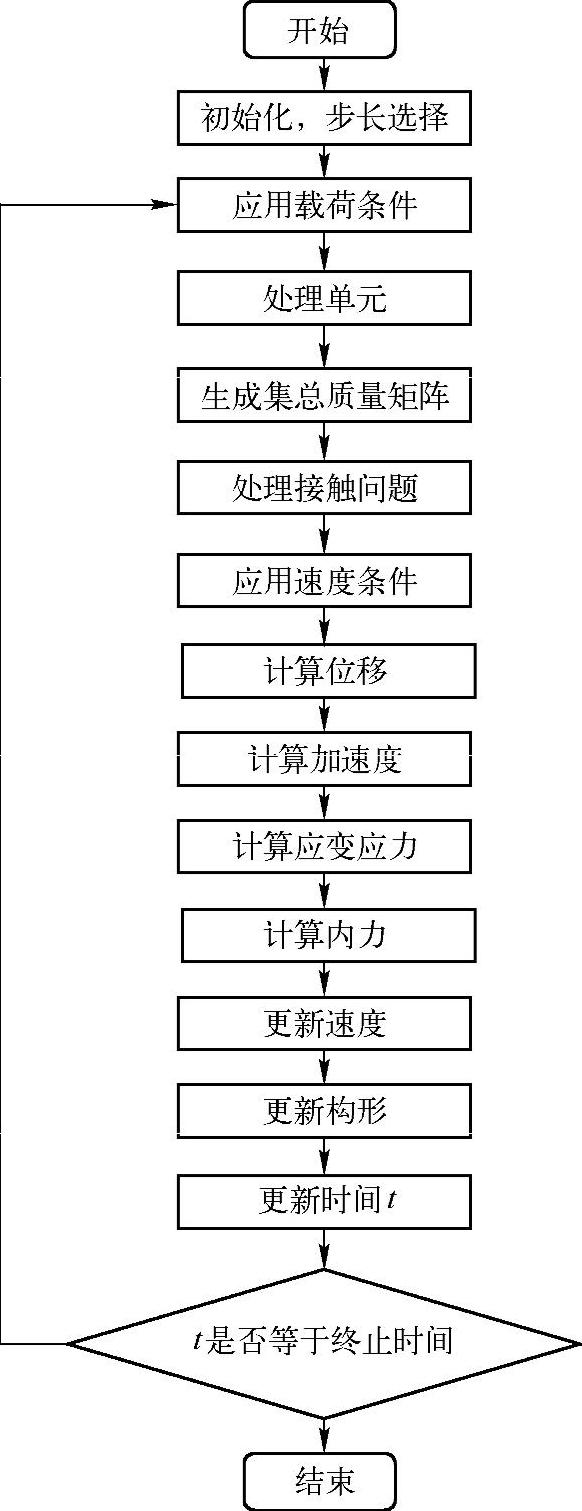
图14-2 非线性动力学有限元求解流程

除了下节讨论的中心差分算法的稳定性条件，还有以下两点需要强调：(www.xing528.com)

（1）中心差分算法是显式算法。K矩阵不出现在递推式（14-18）的左端，当M是对角阵，C可以忽略或也是对角矩阵，利用递推公式求解运动方程时不需要进行矩阵求逆，仅需要进行矩阵乘法运算以获得方程右端的等效载荷，之后可得到唯一的各个分量。显式算法的这个优点在非线性分析中意义突出。因为非线性分析中，每个增量步的刚度矩阵是被修改的，这时采用显式算法可以避免矩阵求逆运算。

（2）中心差分算法比较适用于有冲击、爆炸类型载荷引起的波传播问题的求解是由其算法本质决定的。因为当介质的边界或内部某个小的区域受到初始扰动后，是按一定的波速c逐步向介质的内部和周围传播的。如果分析递推式（14-18），将会发现当M和C是对角矩阵时，即显式算法时，若给定某些节点初始扰动（即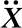的某些分量为非零值），在经过一个时间步长t后，和它们相关的节点（在K中处于同一带宽内的节点）将进入运动，即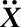中和这些节点对应的分量将变成非零项。随着时间的推移，其他节点将依次进入运动。此特点正好和波传递的特点相一致。但从算法方面考虑，为了答案的正确性，每一个时间步长△t中，网格内与新进入计算节点相应的几何区域的扩大应大于波传播范围的扩大（c△t），所以时间步长要受到限制，即小于临界步长△t_cr。当研究高频成分占重要作用的波传播过程时，为了得到有意义的解，必须采用小的时间步长。这也是和中心差分算法的时间步长需要受到临界步长限制的要求相一致的。