采用U.L.格式,利用虚功原理建立的非线性动力学有限元控制方程为

式中,M为质量矩阵。
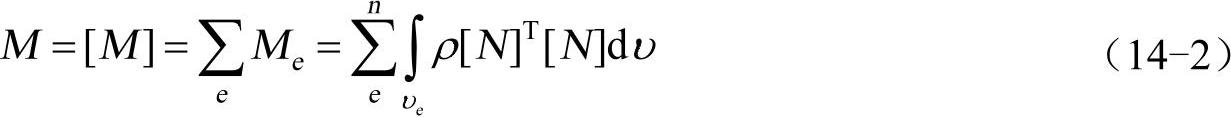
n为单元总数,[N]为插值矩阵(形函数矩阵)。
C为阻尼矩阵。
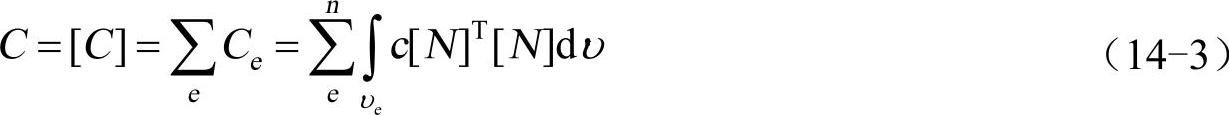
K为总体刚度矩阵。
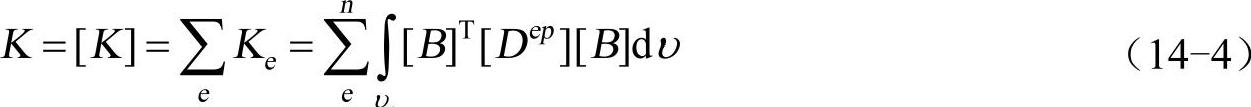
Fext为外力矢量。
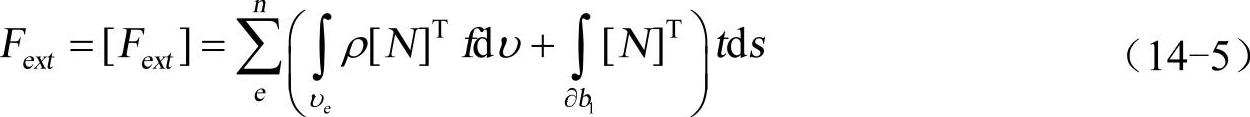
f为单位质量的体力矢量。

t为面力矢量。

f为接触力矢量,是法向接触力和切向摩擦力的合力。
cx、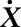 和
和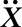 分别为位移矢量、速度矢量和加速度矢量。
分别为位移矢量、速度矢量和加速度矢量。

Kx代表集总内力矢量,其由全局坐标系中单元节点力矢量和力矩矢量确定。
为简单起见,在式(14-1)中令Q=Fext+fc,表示包含接触力的外力矢量,则

把总积分时间分成若干步,每步间隔为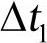 ,
,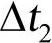 ,…,
,…,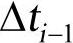 ,
,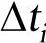 ,
,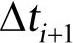 ,…在某一时刻t,其前一步和下一步的时刻如图14-1所示。
,…在某一时刻t,其前一步和下一步的时刻如图14-1所示。

图14-1 时间积分划分

t时刻的加速度为
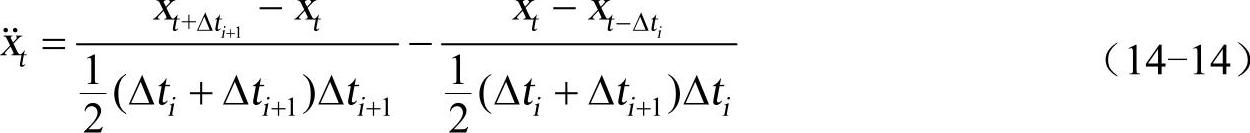 (https://www.xing528.com)
(https://www.xing528.com)
如果总积分时间是均匀分隔的,即有△t1=△t2=…=△ti-1=…△ti=△ti+1=…△t,则得到中心差分算法下的t时刻速度和加速度为
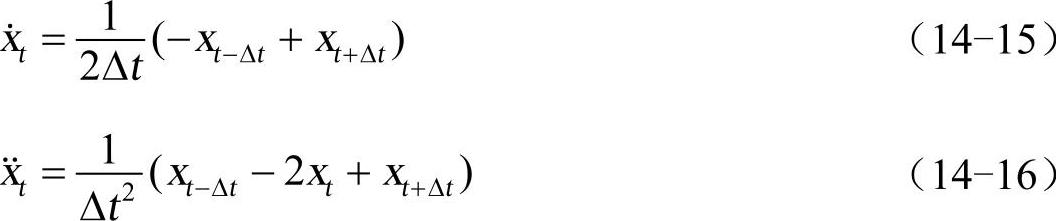
而在t时刻的有限元控制方程为

将t时刻速度和加速度即式(14-15)和式(14-16)代入上式,有
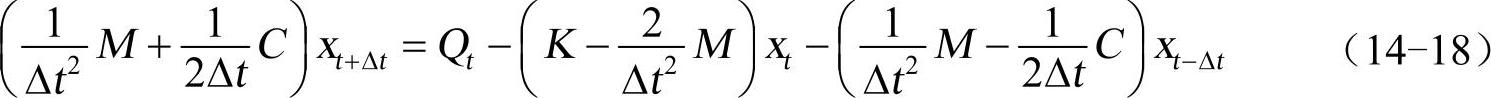
如果xt-△t和xt已经求得,则t+△t时刻的位移xt+△t可以由上式解出,也即上式是求各个离散时间点处解的积分递推公式。由于在t+△t时刻时用的是t时刻的控制方程(式14-17),K矩阵不出现在上述递推公式的右端,所以这种求解过程被称为显式积分算法。
由上述递推公式可知,中心差分算法有一个起步问题。因为t=0时刻,为了计算xt,除了已知的初始条件x0外,还需要知道x-△t,所以必须要用一个专门的起步方法。事实上,利用式(14-15)和式(14-16),可得

上式中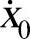 可以从给定的初始条件式
可以从给定的初始条件式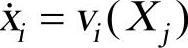 得到,而
得到,而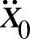 则可以利用t=0时刻的有限元控制方程(式14-17)得到。
则可以利用t=0时刻的有限元控制方程(式14-17)得到。
中心差分算法逐步显式求解有限元控制方程的一般步骤如下:
1.初始计算
(1)形成刚度矩阵K,质量矩阵M和阻尼矩阵C。
(2)给定x0、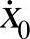 和
和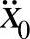 。
。
(3)选择积分时间步长△t,△t<△tcr,并计算积分常数。
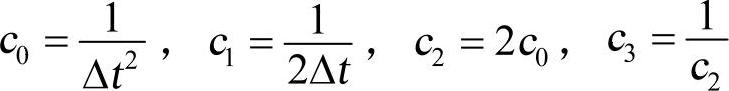
(4)计算选择积分时间步长△t,△t<△tcr ,并计算积分常数。
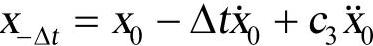
(5)形成等效质量矩阵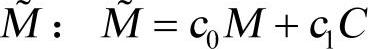 。
。
(6)三角分解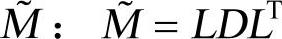 。
。
2.对于每一个积分时间步长
(1)计算时刻t的等效载荷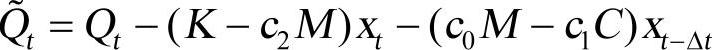 。
。
(2)计算时刻tt的位移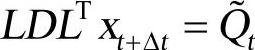 。
。
(3)如果需要,则计算时刻t的速度和加速度。
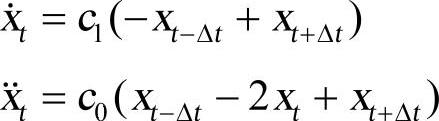
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




