【摘要】:在线性稳态分析中,材料的属性都是线性的,而且主要关心结构在热平衡稳态时的温度和热流量。基本的有限元分析方程式为式:式中,是传热系数矩阵,是自然对流的边界换热系数矩阵,{T}是未知的节点温度,{P}是热载荷向量。高斯消元法利用矩阵的对称性和稀疏性提高了计算效率。表10-1 传热分析和结构分析的对比表热载荷和边界条件在输入文件的Bulk Data部分定义。
传热分析主要求解热载荷作用下结构未知的温度和热流量。温度表征了可用热量的多少,热流量表征了热量流动的快慢。热传递的热量交换是通过分子运动实现的,固体与其周围的流体之间的热量交换是通过自然对流实现的。热载荷以流入和流出系统的热流量大小的方式定义。
在线性稳态分析中,材料的属性(如传热系数和对流系数等)都是线性的,而且主要关心结构在热平衡稳态时的温度和热流量。基本的有限元分析方程式为式(10-1):

式中,(Kc)是传热系数矩阵,(H)是自然对流的边界换热系数矩阵,{T}是未知的节点温度,{P}是热载荷向量。求解系统的线性方程可以得到节点温度{T}。
热载荷向量可以表示成式(10-2):

式中,{pB}是边界热通量功率,可以在QBDY1卡片中定义;{pH}是自然对流的对流向量,在CONV卡片中定义;{pQ}是内部生热的功率向量,在QVOL卡片中定义。
在没有定义温度边界条件的情况下,方程式(10-1)左边的矩阵是奇异的。利用高斯消元法求解平衡方程得到未知温度。高斯消元法利用矩阵的对称性和稀疏性提高了计算效率。计算出节点处的温度之后,就可以根据单元的形函数计算出温度梯度{VT}。单元的热流量可以用式(10-3)计算:(https://www.xing528.com)

式中,(k)是材料的传热矩阵。
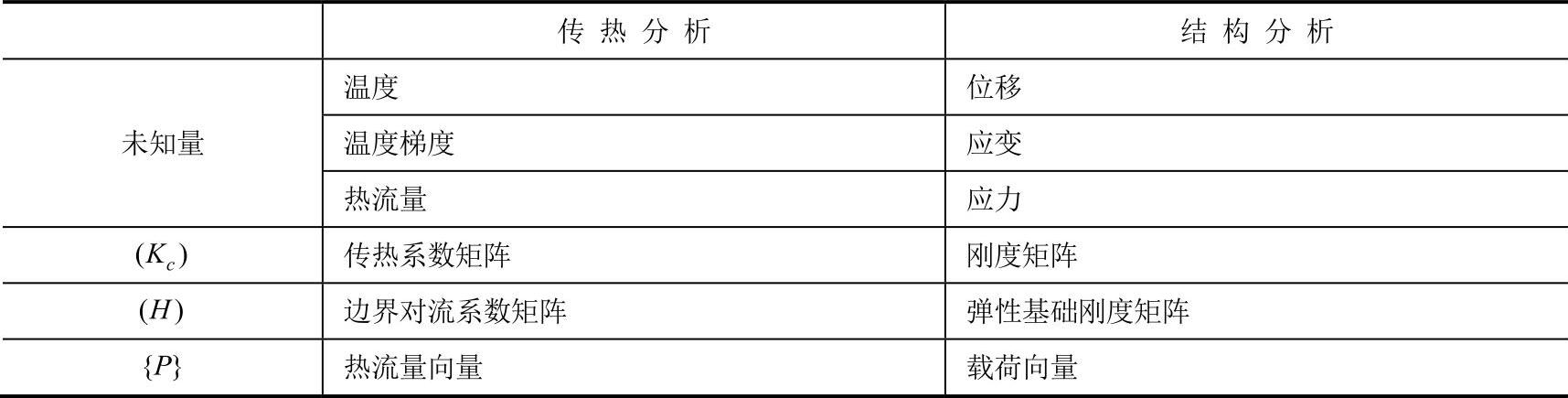
关于传热分析和结构分析的对比如表10-1所示。
表10-1 传热分析和结构分析的对比表
热载荷和边界条件在输入文件的Bulk Data部分定义。它们需要分别以SPC或MPC的形式和LOAD的形式被SUBCASE引用。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




