瞬态响应分析基本理论

瞬态响应分析的载荷可以是与时间相关的力、位移、速度和加速度。初始条件可以定义网格点的初始位移和初始速度。瞬态响应分析的结果是与时间相关的位移、速度、加速度、力、应力和应变等。

瞬态响应分析通过求解式（8-1）～式（8-3）包含以矩阵形式出现的初始条件的运动方程计算结构响应。

其中，矩阵K是全局刚度矩阵，矩阵M是质量矩阵，矩阵B是阻尼单元确定的阻尼矩阵。初始条件是问题公式化的一部分并且仅适用直接法瞬态响应分析。运动方程使用Newmark beta方法在时间域上积分。求解需要定义时间步长和终止时间。

瞬态响应分析求解可使用直接法和模态法。选择直接法进行瞬态响应分析时运动方程应用Newmark beta方法直接求解。在瞬态响应分析中不能用复系数来表示阻尼。因此，结构阻尼需要转换成等效粘性阻尼。

阻尼矩阵B由式（8-4）中的3个部分组成：

式中，B1为粘性阻尼器单元矩阵，G是全局结构阻尼（PARAM,G），W₃是全局结构阻尼转换成等效粘性阻尼所感兴趣的频率（PARAM,W₃），W₄是单元结构阻尼转换成等效粘性阻尼所感兴趣的频率（PARAM,W₄），K_E由结构单元阻尼系数GE确定。

瞬态响应载荷和边界条件在输入文件的Bulk Data段定义。它们必须在SUBCASE段使用SPC和DLOAD引用。直接法瞬态分析不能使用惯性释放。如果使用将会出错。瞬态响应分析仅能定义一个瞬态工况。初始条件必须被SUBCASE声明中的IC引用。分析的时间步长和终止时间必须被SUBCASE声明中的TSTEP（TIME）引用。除了各种阻尼单元和材料阻尼，还可以使用PARAM和G来定义全局结构阻尼G。

选择模态法进行瞬态响应分析时，首先执行模态分析来获得系统的特征值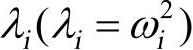和相应的特征向量。方程中u可以表达为特征向量X和模态响应d的内积，见式（8-5）：

u= Xd (8-5)

无阻尼的运动方程通过特征向量变换到模态坐标下，见式（8-6）：

模态质量矩阵和模态刚度矩阵是对角矩阵。这样系统方程就简化成一组d的分量的非耦合方程，很容易求解。

有阻尼的运动方程见式（8-7）：

这里，矩阵通常是非对角矩阵。因此，该耦合问题可以使用类似直接法求解，但方程包含更少的自由度。简化后的运动方程使用Newmark beta方法求解。

假如阻尼单独施加在各个模态点，方程依然是可以解耦的。这个通过阻尼表格TABDMP1来完成，表格中列出了阻尼值g_i相对的固有频率f_i。

解耦后的方程见式（8-8）或式（8-9）：

或者

式中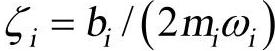，是模态阻尼系数，ω_i是模态特征值。

可以定义3种类型的模态阻尼值G_i（f_i）：G—结构阻尼，CRIT—临界阻尼，Q—损耗因子。它们的关系见式（8-10）～式（8-12）（与频率响应分析相同）：(www.xing528.com)

通过在特征向量矩阵X上增加位移向量（基于动载荷的静态分析得到），模态分析的精确度可以大幅度地提高。这些向量常常被称为残余矢量，该方法称为模态加速方法。关于残余矢量的详细介绍请参考频率响应部分。

瞬态响应载荷和边界条件由输入文件的Bulk Data段定义。它们必须在SUBCASE中使用SPC申明和DLOAD申明引用。

如果使用模态法求解则不能定义初始条件。对于模态法需要一个METHOD申明去控制模态分析方法。分析时间步长和终止时间必须通过SUBCASE段的TSTEP（TIME）引用。为了节省计算量，通过使用SUBCASE段的EIGVRETRIEVE申明可以重新获得之前保存的特征向量。还可以使用傅里叶变换，可以用频率响应分析方法来做瞬态分析。傅里叶变换方法可以用来解决结构模型在周期性载荷作用下的瞬态响应。这种方法的典型应用是汽车在颠簸路面上行进。

时间相关的载荷被转换成频域内，所有频率相关的矩阵计算都完成之后频率响应结果再转换到时域内。

结果是位移、速度、加速度、力、应力和应变，通常是时间相关的。

初始条件为矩阵形式的运动方程求解见式（8-13）：

这里矩阵K是刚度矩阵，矩阵M是质量矩阵，矩阵B是阻尼单元确定的阻尼矩阵。

载荷向量使用式（8-14）中的方法从时域转换成频域：

响应结果见式（8-15）：

式中，h（Ω）是单位载荷下的频率响应。

频率响应分析之后，可以通过式（8-16）还原为时间相关的响应：

为了结果的准确性，需要注意以下几点。

（1）系统必须有合理的阻尼，太小的阻尼将导致不正确的结果。

（2）为了允许延迟，某些时间间隔的强制函数应该为0。

（3）频率间隔应该遵循。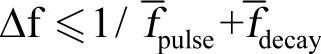

可以使用直接法和模态法求解。分析时间步长和终止时间必须通过SUBCASE段的TSTEP（FOURIER）引用。