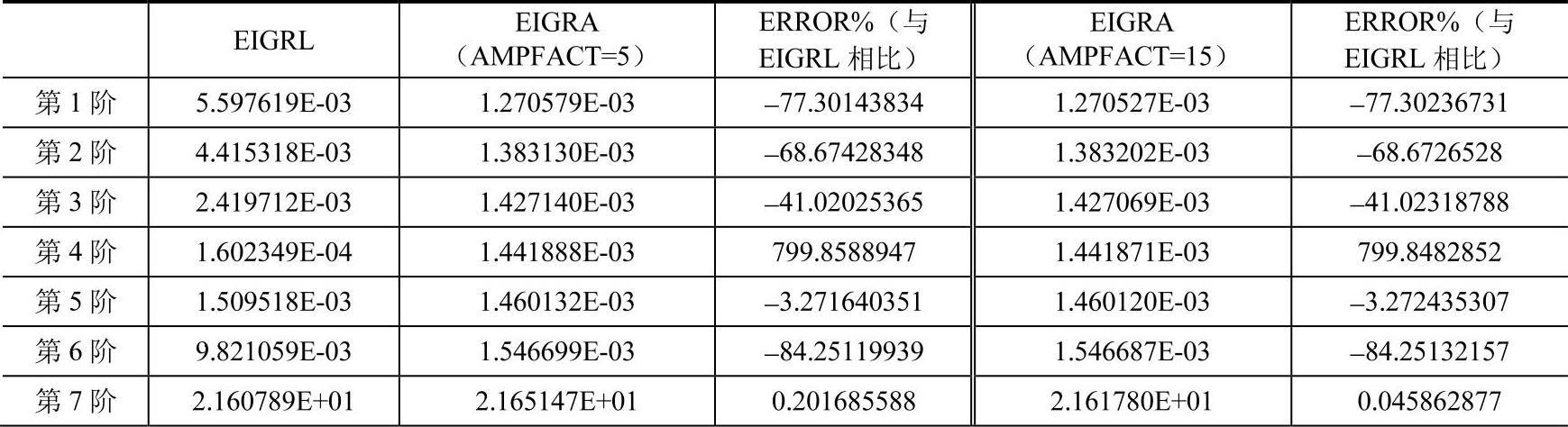
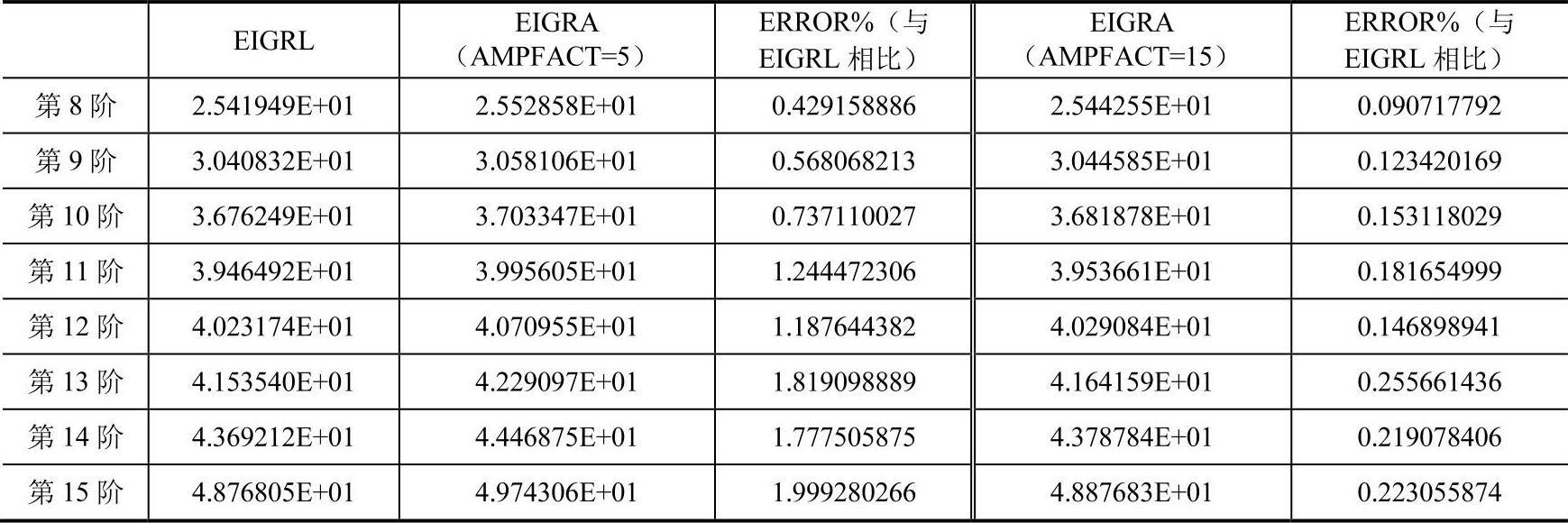
【摘要】:对于本章6.2.2节中的白车身模型,如果使用EIGRA时,与EIGRL相比,第1阶非刚体模态的频率误差为0.2%,而且随着阶数的提高,误差不断积累,越来越大,第9阶非刚体模态的频率误差达到了2%;使用EIGRA时,与EIGRL相比计算时间有所增加,第1阶非刚体模态的频率误差不到0.05%,同样随着阶数的提高,误差不断积累,越来越大,第9阶非刚体模态的频率误差为0.23%。
这里的模态加速技术指自动多级子结构特征值求解方法(AMSES)。
在AMSES方法中每次只计算一个部分的特征向量。该方法对硬盘空间和I/O的需求都大幅度减小。因此,与EIGRL方法相比所需的计算时间要短得多。对于典型的NVH分析,关心的自由度一般只有100个左右。使用这种方法百万自由度的模型的求解只需要几个小时。AMSES方法的不足之处在于,它的求解是不精确的,但是模态频率的精度依然可以达到小数点后几位。对于NVH分析来说,模态空间中的模态振型能够覆盖到尽可能多的变形模式比每一阶模态的值的精度更为重要,所以使用AMSES方法完全可以满足工程上对精度的要求。
对于本章6.2.2节中的白车身模型,如果使用EIGRA(AMPFACT=5默认值)时,与EIGRL相比,第1阶非刚体模态的频率误差为0.2%,而且随着阶数的提高,误差不断积累,越来越大,第9阶非刚体模态的频率误差达到了2%;使用EIGRA(AMPFACT=15)时,与EIGRL相比计算时间有所增加,第1阶非刚体模态的频率误差不到0.05%,同样随着阶数的提高,误差不断积累,越来越大,第9阶非刚体模态的频率误差为0.23%。
总之,参考EIGRL的结果,使用EIGRA时,增大AMPFACT可以提高精度(计算时间有所增加),提高截断频率可以降低精度。
使用EIGRA和EIGRL计算得到的结果对比如表6-17所示。(https://www.xing528.com)
表6-17 EIGRA和EIGRL计算结果对比
(续)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




