RADIOSS线性屈曲分析理论及应用

使用有限元方法求解线性屈曲问题，首先在结构上施加一个参考载荷P_ref，然后通过线性静态分析得到结构应力，该应力将用于后面的几何刚度矩阵K_G的构建。最后通过求解特征值问题得到屈曲因子，计算的方程见式（4-1）：

K是结构的刚度矩阵，λ是参考载荷的放大系数。通常求解特征值问题可以得到n个特征值（n是系统的自由度数），但实际中通常只求解少量的特征值；x是与特征值对应的特征向量。

求解特征值问题使用Lanczos方法。该方法只求解较低阶的一些特征值。最小的λ与结构屈曲有关，因为一旦发生屈曲结构已经失效，所以通常情况不需要考虑后面的特征值。屈曲临界载荷可以根据式（4-2）计算：

为了进行线性屈曲分析，需要在Bulk Data段定义一个EIGRL卡片用于定义特征值提取阶数。EIGRL卡片需要被SUBCASE段的METHOD引用。另外，还需要使用SUBCASE段的STATSUB引用参考的静态分析工况。线性屈曲分析不能使用惯性释放选项。

屈曲分析忽略0维单元，如MPC、RBE3和CBUSH。它们可以在线性屈曲分析中使用，但不参与几何刚度矩阵K_G 的构建。默认情况下，几何刚度矩阵K_G的构建也不考虑刚性单元的影响。如果希望考虑刚性单元的影响，可以通过设置PARAM、KGRGD和YES实现。

另外，用户也可以通过SUBCASE段的EXCLUDE指定几何刚度矩阵K_G构建时忽略的一些其他单元，这样可以指定只对部分的结构进行屈曲分析。EXCLUDE指定的部分只是在构建几何刚度矩阵时被忽略，相当于一个带弹性边界条件的分析。所以，被排除部分仍然会在屈曲模态结果中有运动。(www.xing528.com)

如果参考的静态载荷工况使用了惯性释放，则不能使用屈曲分析。因为在这种情况下刚度矩阵是半正定的，屈曲分析会由于矩阵奇异而终止。

某些1D单元和壳单元可以通过设定偏置，将由单元节点位置定义的原始位置的单元刚度矩阵进行转换。例如，壳单元可以通过ZOFFS沿法向偏移到单元平面以外的位置。在这种情况下，计算应力使用的材料矩阵或者纤维位置都是根据偏置参考平面定义的。类似的，单元力也是在偏置参考平面定义内输出的。

偏置用于所有单元矩阵（刚度、质量、几何刚度矩阵以及各种单元载荷，如重力），原则上说偏置可以用于包括屈曲分析在内的各种分析和优化，但是在解读结果的时候要慎重。因为如果没有偏置，一个典型的简单结构在临界载荷的作用下会立即分叉并失去稳定性，如图4-1a所示。如果有偏置，结构的稳定性会逐步失去，渐进地达到临界载荷，如图4-1b所示。

在实际中，使用偏置的结构在临界载荷达到之前可以有很大的变形（例如框架类结构或承弯的结构，即使不在单元卡片中使用ZOFFS也会以极限载荷的形式发生屈曲）。此外，对于完全非线性方法，在极限载荷路径上可能出现其他的不稳定点。

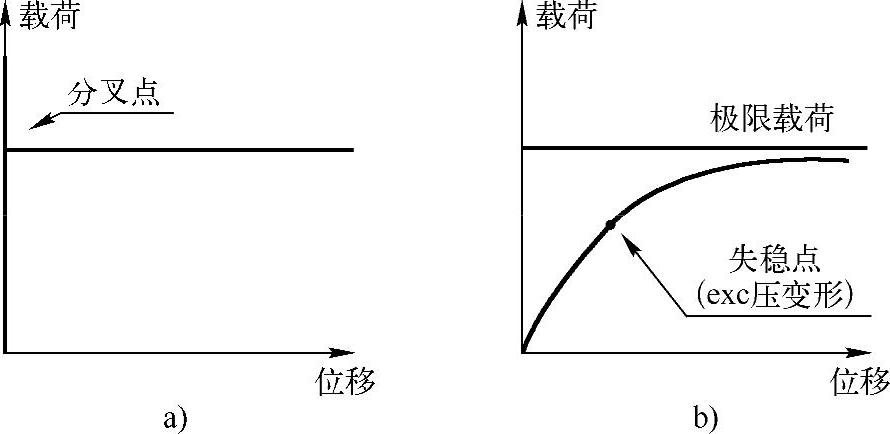
图4-1 结构变形载荷图