我的数学课堂：系统有温度

数学本就是一个极具系统性的科学，我们的课堂教学，不能将其割裂开。

（1）大单元设计。数学本就是一个具有系统性的科学，因此在教学中，我们对整个单元的教学要有系统性的设计，要厘清知识模块的脉络，才能明白某一概念在整体中的地位、作用，联系学情，合理安排课时。例如，必修2 立体几何模块《点、直线、平面之间的位置关系》。这一章节是立体几何模块的主体，提出了立体几何模块最基本的公理和定理体系，建立了立体几何的基本理论框架。学习整章，首先要厘清知识脉络，课本的大体框架首先是建立平面概念，规定空间的表示法和叙述规范，建立公理体系；然后是从公共点个数的角度来定义点、线、面之间的位置关系，给出空间平行关系的判定和性质定理；最后是给出空间垂直关系的定义、判定和性质定理，以及线面角和二面角的概念。其次应当针对学生的学情，帮助学生整理所有平行关系、垂直关系、空间角。例如，针对学生一直非常困惑的垂直问题，我帮助学生作关于空间垂直关系的所有定理的思维导图，还设计了通过一系列“寻找垂直关系”的问题，来帮助学生构建空间垂直关系。

大单元设计有助于我对章节、知识模块的整体把握，也能在授课中让学生体会到整个章节的系统性。学生在章节学习中可能会碰到多个课时中比较相近的难点系列，而大单元设计可以整合多个课时的内容，对这些系列难点进行梳理，从系统上进行突破。

（2）前后概念的联系。这种系统性还体现在数学概念的教学中，体现在数学概念产生的必要性上。任何数学概念的产生、发展都不是孤立的，它或因为前序概念的延伸、拓展，又或是后序概念的需要而形成。因而，在我们的概念教学中也应体现这一点。由前序概念的延伸、拓展、类比中产生新的数学概念，是很多教师普遍采取的教学策略，本人的拙作《增删问题步骤揭示数学本质》中也提及了“组合”与“排列”之间的联系。但是数学中仍然存在着大量这样的概念，它的提出非常突兀，看似不自然、不合理，但在后序的研究中却是如此的必要和自然。例如函数中奇偶性、单调性的提出，完全是教师的引导。但是这两个性质在函数的研究中是如此重要，所以，通常我会在后序的问题中设计这样的环节：

问题1：请作出函数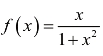的简图。

其实很多时候，教师选题不要特意去选难题、复杂问题，往往揭示数学深刻思想的是一些看起来很简单的问题。关于这个问题深刻性的论述，我会在后文中详述，此间只谈对奇偶性、单调性两个概念合理性的阐述。

学生：函数f（x）是奇函数，关于原点对称，并且在（0，1）上递增，（1，+∞）上递减。（作图）

我会追问在我们解决这个问题的过程中，研究函数的奇偶性与单调性，会给我们带来了什么好处？此问题给我们对陌生函数进行研究提供了哪些帮助？

学生：奇偶性给出了函数整体上的性质，减少了我们需要研究的区间长度，（-∞，0）上的图像可由对称性给出。单调性解决了函数变化的趋势，指出了函数的最值。这两个性质对于函数性态的研究起了关键的作用。对于陌生函数，我们可以先确定它的定义域，再研究它的奇偶性（对称性）和单调性，解决它在每一个单调区间内的最值，就可以作出函数的草图了。

我：所以奇偶性和单调性的概念对函数研究是至关重要的。这两个概念在一开始提出或许是突兀的，但是现在看来确实极其必要。

在我看来，很多的数学概念并不能由教师引导得出，事实上也没这个必要。如果所有数学概念都能由教师引导得出，那么数学也不需要经历这上千年的发展，也没必要出现欧拉等天才的数学家。但是，我们应该了解他们提出的概念、方法，理解他们的思想，感慨他们伟大的前瞻性。正如必修1 人教A 版的主编寄语中提到“数学是自然的”，“如果有人感到某个概念不自然，是强加于人的，那么只要想一下它的背景，它的形成过程，它的应用，以及它与其他概念的联系，你就会发现它实际上是水到渠成、浑然天成的产物”。(www.xing528.com)

（3）性质、定理的递进承接顺序。数学的系统性还体现在对于性质、定理的递进关系的解析上。梳理性质之间的关系，能让学生对数学的理解更有条理性。例如，在不等式的基本性质中，教材给出了6 个性质：

①若a ＞b，则b ＜a；若b ＜a，则a ＞b；

②若a ＞b，且b ＞c，那么a ＞c；

③若a ＞b，那么a+c ＞b+c；

④若a ＞b，且c ＞0，那么ac ＞bc；

若a ＞b，且c ＜0，那么ac ＜bc；

⑤若a ＞b ＞0，那么an ＞bn（n ∈N，n ＞1）；

⑥若a ＞b ＞0，那么（n ∈N，n ＞1）。

看起来是极其简单的事实，有的教师在此处可能选择将6 个性质读一遍就过了。但是在我看来，这里却蕴藏着对数量关系研究的基本问题。大于、等于、同余（数论）、相似、合同（线性代数）等都是数量（可能是多维的）之间的基本关系，它们的性质研究基本类同。对比其他，我们会发现不等式性质，其实缺了第一条，反身性，即一个变量与其自身是否具有这层关系，显然我们不可能有a ＞a，这也是为什么在不等式基本性质中反身性不提的缘由。这一点，我会在课堂上指出。另外，我们还可了解为什么不等式的性质会有这么多条，事实上，除反身性是数量与自身关系外，①②两条数量的维度是逐渐增多的，①表达了两个数量之间是否可交换位置，我们称为对称性；②表达了三个数量之间的关系能否传递，我们称为传递性；③④加入了四则运算研究，③称为加法单调性；④为乘法单调性；⑤为④的拓展，乘方运算单调性；⑥中的开方是⑤中乘方的逆运算。7 个性质（加上不成立的反身性）的递进、承接是一个系统且完整的研究数量关系的过程，我会在课堂上为学生指出，并要求以后遇到新学的数量关系，要类比不等式性质系统地研究。类似的问题，还有向量的内积的运算律。