树：连通无回路的无向图称为无向树，简称树，常用T表示.在树中，悬挂结点称为树叶，度数大于1的结点称为分支点或内结点，悬挂边称为叶边.连通分支数大于1，且每个连通分支都是树的无向图称为森林.
定理9.28 设T=＜V，E＞是n阶m条边的无向图，则下面命题等价：
（1）T是树.
（2）T无回路且m=n-1.
（3）T连通且m=n-1.
（4）T是连通的，且T的每条边都是割边.
（5）T无回路，但任意增加一条边产生唯一一条回路.
（6）T中每对结点间恰有一条路.
定理9.29 若T=＜V，E＞是树，且|V|≥2，则T中至少存在两片树叶.
生成树、弦：若T是连通无向图G的生成子图且是树，则称T是G的生成树.G在T中的边称为T的树枝，G不在T中的边称为T的弦.
定理9.30 无向图G=＜V，E＞有生成树当且仅当G是连通的.
定理9.31 若T是连通图G的任意生成树，则G的每个边割集和T至少有一条公共边.
生成树的权、最小生成树：设连通无向带权图G=＜V，E，W＞，T是G的一棵生成树，T的各边带权之和称为T的权，记为ω（T）.G的所有生成树中带权最小的生成树称为最小生成树.
Kruskal算法：
（1）在G中选取最小权边e1，并置边数i=1.
（2）当i=n-1时结束，否则转向（3）.
（3）设已选择的边为e1，e2，…，ei，在G中选取不同于e1，e2，…，ei的边ei+1，使得ei+1是满足与e1，e2，…，ei不构成回路且权值最小的边.
（4）置i为i+1，转向（2）.
Prim算法：
（1）在G中任意选取一结点v1，并置U=｛v1｝，置最小生成树的边集TE=｛｝.
（2）在所有u∈U，v∈V-U的边［u，v］∈E中，选取权值最小的边［u，v］，将［u，v］并入TE，同时将v并入U.
（3）重复（2）直到U=V为止.
根树：给定一个有向树，若只有一结点入度为0，其余结点入度都为1，称其为根树.入度为0的结点称为树根，入度为1出度为0的结点称为树叶；入度为1出度大于0的结点称为内结点.内结点和树根通称为分支点.从树根到其某个结点的路径长度，称该结点的级或层次，其最大者称为有向树的树高.(www.xing528.com)
有序树：将根树每一级上的结点规定次序，这样的根树称为有序树.
m叉树：T为一棵根树，若T的每一分支结点至多m个儿子，称T为m叉树.若T的每一分支结点恰有m个儿子，称T为完全m叉树.若所有叶结点级相同，称T为正则m叉树.
树转化为二叉树的方法：
（1）从根开始，保留每个父亲同其左边孩子的连线，撤销与别的儿子的连线.
（2）兄弟间用从左到右的有向边连接.
（3）选定二叉树的左儿子和右儿子如下：直接处于给定结点下面的结点作为左儿子，对于同一水平线上与给定结点右邻的结点，作为右儿子，依次类推.
先序遍历法：访问树根、先序遍历左子树、先序遍历右子树.
中序遍历法：中序遍历左子树、访问树根、中序遍历右子树.
后序遍历法：后序遍历左子树、后序遍历右子树、访问根树.
最优二叉树：设二叉树T有t片树叶，分别带权ω1，ω2，…，ωt，称ω（T）=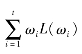
为T的权，其中L（ωi）为从根结点到带权ωi的树叶的通路长度.在所有带权ω1，ω2，…，ωt的二叉树中，带权最小的二叉树称为最优二叉树.
定理9.32 设T为带权ω1≤ω2≤…≤ωt的最优二叉树，则
（1）带权ω1，ω2的树叶v1，v2是兄弟.
（2）以树叶v1，v2为儿子的分支点，其通路长度最长.
定理9.33 设T为带权ω1≤ω2≤…≤ωt的最优树，若将以带权ω1和ω2的树叶为儿子的分支点改为带权ω1+ω2的树叶，得到一棵新树T′，则T′也是最优树.
Huffman算法：
给定实数ω1，ω2，…，ωt且ω1≤ω2≤…≤ωt，则按下列步骤求最优二叉树：
（1）连接ω1，ω2为权的两片树叶，得一分支点，其权为ω1+ω2.
（2）在ω1+ω2，…，ωt中选两个最小的权，连接它们对应的结点（不一定都是树叶），得分支点及所带的权.
（3）重复（2）直到形成t-1个分支点，t片树叶为止.
前缀码：设β=α1α2…αn是长度是n的符号串，称其子串α1，α1α2，…，α1α2…αn-1分别为β的长度为1，2，…，n-1的前缀.设B=｛β1，β2，…，βm｝为一个符号串集合，若对任意的βi，βj∈B，i≠j，βi和βj互不为前缀，称B为前缀码.若βi中只出现2个符号（如0、1），则称B为2元前缀码.
定理9.34 任何一棵二叉树的树叶对应一个前缀码.任何一个前缀码对应一棵二叉树.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
