回归方程显著性检验的结果

建立了回归方程以后，方程的回归效果如何呢？它是否真实地反映了变量之间的线性关系呢？为此，我们需要对回归方程的有效性进行检验才能加以肯定或否定。对回归方程显著性检验的目的在于保证方程存在线性关系，其检验方法有多种，如回归系数b检验，对回归方程整体的检验判定（方差分析），估计标准误差的计算，测定系数和相关系数的拟合程度的测定。对于线性回归方程来说，最常用的显著性检验是方差分析法。

因变量变异的原因及分解：

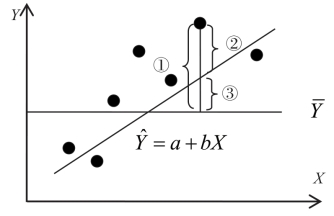
图10-4　线性回归变异分析示意图

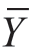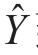上图（10-4）中可以直观地看出Y值的几个变异来源。散点图中任意一点Y到的距离①可以分成两部分：一部分是该点Y到回归线的距离②，另一部分是该点的估计值到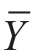的距离③。即：

如果各点都接近回归线，则（Y-）很小，（Y-）中绝大部分都是（-），这种情况说明各点与回归线的误差很小，回归方程有效。

将公式（10-15）两边平方，再对所有点求和，则有：

∑（-）2是总平方和中已被X与Y的线性关系所说明的那部分，称作回归平方和，记为SSR；

∑是指偏离回归线的平方和，称作误差平方和，记为SSe。

则有：总变异=回归变异+误差变异，即SSt＝SSe+SSR 。

若用原始数据计算三个平方和，则有：

各种变异的自由度如下：

对于所有的Y值，自由度为n-1，即dft＝n-1。

在回归平方和值的计算不但要用到，还需要用到b，所以此时Y值失去两个自由度，即dfe＝n-2，因此，dfR＝dft-dfe＝1。

做F检验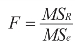：或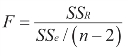

通过F检验，判断MSR是否显著大于MSe，如果MSR显著大于MSe，则表明总变异中回归的贡献显著，或称回归方程显著。(www.xing528.com)

请看下面的具体例子：

例：下表中的16对数据是为确定中考数学成绩与某心理量之间的关系而做的实验的结果。假设两者呈线性关系，且已求出以X估计Y的回归方程为：=.X-.091374。试对这一回归方程进行显著性检验。

表10-3　16名被试中考数学成绩（X）与某心理量（Y）

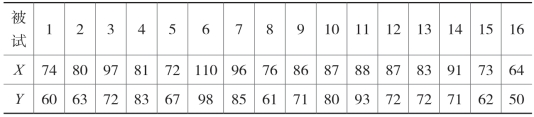
解：（1）建立检验假设

H0：方程无显著线性关系。

H1：方程有显著线性关系。

（2）方差分析

求平方和：

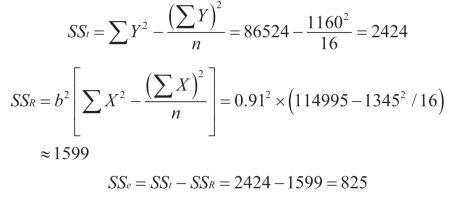
求F值：

（3）比较与决策

因为F ＞F0.01（1，14），p＜001，差异极显著。所以拒绝H0，接受H1，说明所建立的方程存在极显著的线性关系。

（4）列方差分析表