原始数据求回归系数-教育与心理统计学

要求得回归方程进行预测，必须先求回归系数，求得回归系数，回归方程就得到了，回归直线也就被确定了。

最优配合线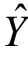=a+bX，须满足为最小的条件，并根据这个条件确定a及b的值。将ˆY=a+bX代入，因而。目前的问题是怎样求a和b的值，才能使上式为最小。在上式中，a与b均为未知数，故上式可以用G（a，b）表示，即：

若要求a与b使上式数值为最小，则上式对a及b的偏导数必须各等于0，即a与b必须满足下列两个方程式：

上式展开并整理，则得：

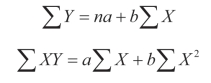
上列n指数列项数，这两个联立方程式，是决定a和b值的两个条件，称为标准方程式。用消去法，可得下列公式：

由X估计Y的回归系数：

同理，由Y估计X的回归系数：

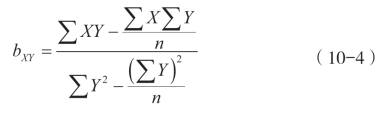
（10-3）式中bYX即指X为自变量Y为因变量，是Y对X的回归系数。（10-4）式中bXY即指Y为自变量X为因变量，是X对Y的回归系数。

根据标准方程式：

则可得

同理

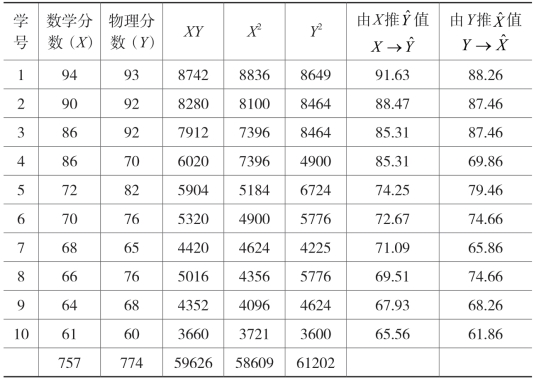
现以表10-2的资料为例，求Y对X的回归系数。

表10-2

(www.xing528.com)

已知n=10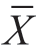，=75.7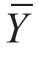，=77.4。

将表中数值代入公式（10-3），得：

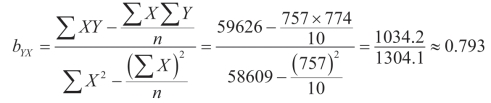
（或0.79）

将上列数值代入（10-5）公式，得：

aYX与bYX均可求出，代入（10-1）即得到Y对X的回归方程。并可根据X值求出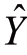值。

Y对X的回归方程为：

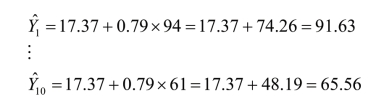
用同样方法将表中数值代入公式（10-4），得：

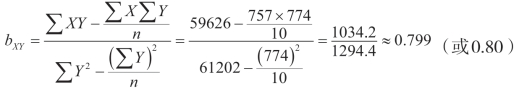
将上列数值代入公式（10-6），得：

bXY与a求出后，代入公式（10-2）即得到X对Y的回归方程，Y为已知，则可求出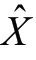值。

X对Y的回归方程为：

图10-2　十名学生数学与物理分数的回归直线

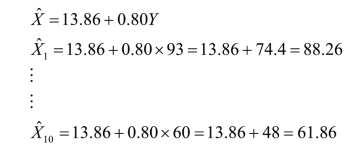
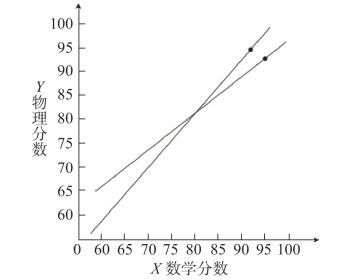
这样，Y对X的回归直线与X对Y的回归直线就可以描绘出来了。回归系数bYX意味着X变量改变一个单位，Y变量也就随之变动bYX个单位。本例就是：当数学改变一个单位，物理分数就改变0.79个单位。同样，bXY意味着Y变量改变一个单位，X变量相应地变动bXY个单位。在本例中，物理改变一个单位，数学分数就改变0.80个单位。本例回归直线如图10-2。