回归线、系数与方程-教育与心理统计学

最能代表诸对变量在分布图上趋势的配合线称为回归线。这条直线的斜率称为回归系数。关于这条直线的方程式，则叫回归方程式。

若要研究许多成对的、不完全相关的变量（X、Y）之间的关系，最简单的方法是把成对的变量用坐标表示，画成散点图。这时，我们可以发现那些散点并不在一条直线上，这些点有一个明显的倾向，即散布在一条直线的周围。如果我们用一根直线在这些散点中移动，当这根直线移动到各点距直线在Y方向的距离的平方和为最小时，该直线就被唯一地确定。符合这个条件的直线就叫回归线。这种求回归线的方法，称为最小二乘法。

例：根据十名学生两次测验的分数求回归直线。

表10-1

假定图10-1中的直线是根据表10-1的资料所求得的回归线，由于该表资料不是完全相关，因而十个散点不是完全落在这条回归线上，而是这些点距这条线的平方和最小。如果十个散点完全落在回归线上，则X与Y是完全相关的，这时就可以用直线方程的通式Y=a+bX来表示这条直线了。但是图10-1上十个散点都没有落在回归线上，这条线只是这些点在附近汇聚的一条配合线。因此，回归线的方程写作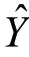=a+bX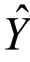（代表Y的估计量）。图10-1只是为了说明回归线而用的很少的资料。事实上，计算相关的二变量是一个正态双变量，计算回归的二变量也应该是一个正态双变量，可以理解为回归线上的各点，都是许多Y值的总体平均数的一个估计量，即一个X值可能对应多个Y值，这些Y值的总体平均数的估计量落在回归线上。

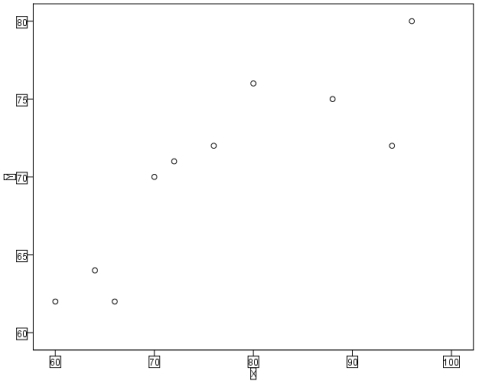
图10-1　表10-1资料以图形表示

以上所说是由X估计Y的回归线，其方程式为：(www.xing528.com)

此外还可以求由Y估计X的回归线，其方程式为：

回归线上的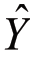值只是Y的估计平均数。它与具有确定关系的X、Y二变量中，一个X值只有一个Y值与之相对应不同。因而回归线上的Y值，称为估计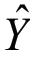（读作y尖）。

由此可知回归线的性质：

1.原数列数值与对应回归线之值的离差平方和为最小，即=最小

2.距回归线的离差之和为0，道理是一样的。