教育与心理统计学：2×2列联表独立性检验

例：从某城市中学和郊区中学中随机抽取一部分学生，调查他们对现行招生制度的看法，结果如表9-2。问城市中学生与郊区中学生对现行招生制度的看法是否有显著差异？

表9-2　2×2列联表

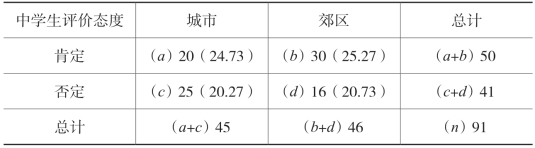
检验步骤如下：

1.建立虚无假设H0：城市生与郊区生对招生制度的看法没有差异

2.计算χ2值

计算χ2值，首先要求出各格的理论次数fe。每一格内的理论次数，等于该格所在行的总次数乘以所在列的总次数除以全部总次数所得的商。公式为：

式中，fe为各格的理论次数；

　　　fr为某一理论次数所在行的总次数；

　　　fc为某一理论次数所在列的总次数；

　　　n为全部总次数。

根据公式（9-2），2×2列联表各格的理论次数分别为：

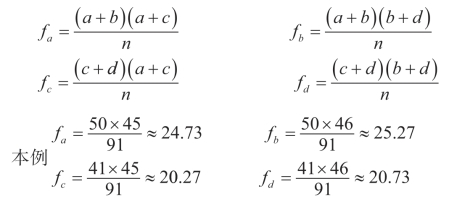(www.xing528.com)

因为2×2列联表的自由度df=2-1=1，计算χ2的值必须用下列校正公式：

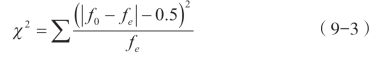
于是本例的χ2值为，

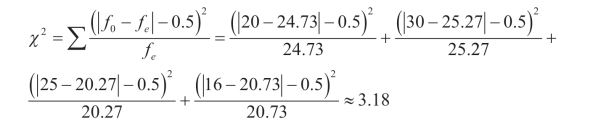
3.确定显著性水平α，查表求临界值χ2α（df）

取α=0.05，df=1，查表得χ20.05（1）=3.84。

4.比较，做出判断

因为χ2=1.613＜χ20.05（1）=3.84，χ2值落入接受区域，因而接受假设H0，即城市中学生与郊区中学生对现行招生制度的看法没有差异。或者说，学校所在地域与学生对招生制度的看法独立无关。

对于2×2列联表，还可以用下列公式直接计算χ2值。公式为：

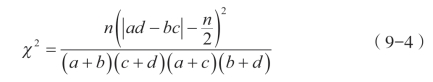
根据表9-2的资料计算

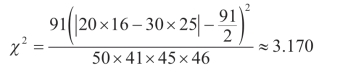
计算结果和按公式（9-3）算得的结果几乎相同。