N-K检验法及其应用

N-K检验法是由Newman和Keuls共同提出的，因此用两人名字的首字母命名。因其检验统计量用q命名，故又称作q检验。该检验方法的具体步骤如下：

1.建立假设

多重比较是逐对检验平均数之间的差异，因此其假设检验也是逐对做出的。通用形式为：

2.求各对平均数的比较等级r

要把被比较的各个平均数从小到大做等级排列，求出每一对平均数之间的比较等级r。r为被比较的两个平均数各自在等级排列中等级之差再加1，即：

3.查q值表确定临界值

根据显著性水平α，比较等级r和自由度df查q值表确定q的临界值qα（r）。这里的显著性水平α应与方差分析中所用的α一致，而自由度就是组内方差MSw的自由度，即df＝N-K。要注意q的临界值不止一个，因为各对平均数之间的跨度数不一样，不同跨度数对应着不同的临界值。在一项具体的检验中，将有K-1个不同的跨度数，因此必须查K-1个q的临界值。

4.计算检验统计量

N-K的检验统计量为q。q检验统计量的公式为：

其中，在完全随机区组设计中，若各组容量不相等，则用下式求SEX：

5.下统计检验结论

将计算得到的各检验统计量q值与查表得到的临界值做比较，但要注意做比较的两个q值应有相同的比较等级。若计算得到的q值小于临界值，则不能拒绝零假设；若计算得到的q值大于临界值，则拒绝零假设，说明两个总体平均数有显著性差异。(www.xing528.com)

例：分别从5所学校中各随机抽取3名学生进行物理测试，其成绩如下表所示。方差分析结果表明，不同学校的学生物理平均成绩显著不一致，其MSw=5.4，dfw=10，请对这5所学校物理平均成绩进行逐对检验。

解：（1）建立假设

（2）把5个平均数排等级，求比较等级。如下表：

rAC=5；rAD=rEC =4；rAB=rED=rBC =3；rAE=rEB=rBD=rDC=2。

（3）查q值表，确定临界值

（4）计算检验统计量qij（r）

用公式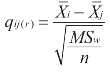可以分别求出各对平均数的q检验统计量的值如下：

同理求得qAB（3）≈5.22；qED（3）≈6.71；qBC（3）≈3.73；qAE（2）≈1.49；qEB（2）≈3.73；qBD（2）≈2.98；qDC（2）≈0.75。

（5）将q值与q临界值进行比较，得出检验结论。如下表所示：

*：p＜0.05，**：p＜0.05

通过以上例题可知，进行方差分析后，我们只是在整体上得出了几个平均数之间是否有显著性差异的结论。并且经过多重比较后才能进一步说明哪两对平均数的差异达到了显著性水平。值得注意的是，多重比较的方法不仅仅限于F检验，只要是对多个平均数进行的两两比较，都应使用多重比较的方法。