教育与心理统计学：方差分析的逻辑

（一）什么是方差分析

方差分析是检验多组样本均值间的差异是否具有统计意义的一种方法。方差分析又称变异分析，通过对多组平均数的差异进行显著性检验，分析实验数据中不同来源的变异对总变异影响的大小。作为一种统计方法，方差分析是把实验数据的总变异分解为若干个不同来源的分量，因而它所依据的基本原理是方差（或变异）的可加性，或者说方差的可分解性。方差分析是将总平方和分解为几个不同来源的平方和（实验数据与平均数离差的平方和）然后分别计算不同来源的方差，并计算方差的比值即F值。根据F值是否显著来判断几组数据的差异是否显著。

（二）方差分析的目的

方差分析又称作变异分析。在前面提到的双总体平均数差异的显著性检验中，我们采用的是T检验或者Z检验，其目的在于检验两个总体平均数之间有无显著性差异。但在实际研究工作中，往往会遇到综合比较三个或三个以上平均数的问题。如果此时继续使用T检验或Z检验进行两两比较，就会使检验的效率降低。因此，我们在对多个平均数进行比较时，常常使用方差分析综合地确定几个平均数差异的显著性，这是一种既不增加犯错误的概率，又不加大工作量的一次性通盘检验方法。方差分析的基本功能就在于对多组平均数差异的显著性进行检验。

（三）方差分析的基本思想

如果把实验获得的多个平行样本的全部数据视为一个整体，则数据之间存在着变异，即参差不齐。造成变异的因素是多方面的，因为每个实验都会受到各种因素的影响，而且有的因素我们不甚了解，有的因素我们无法控制。我们把样本之间由于实验条件不同而引起的实验结果的差异称为组间差异（又称条件误差），把实验条件之外的各种随机因素包括被试之间的个体差异所引起的实验结果的差异称为随机误差，这两部分的差异加起来就构成了实验数据总体的变异。方差分析就是要确定在实验结果的总变异中是否有条件误差存在。

方差分析设法把总变异分解成条件误差（组间变异）和随机误差（组内变异），然后比较二者的关系。如果样本组间变异相对较大，而各样本组内变异相对较小，则认为样本组之间有实质性差异，即条件的改变对实验结果产生显著的影响；如果样本组之间产生的变异与抽样误差等其他原因产生的变异相比较差异不大，则不能认为样本组之间有实质差异，即实验结果的差异主要是由各种随机因素造成的，实验条件的改变对实验结果的影响不大。通过对组间差异与组内差异比值的分析，来推断几个平均数差异的显著性，这就是方差分析的逻辑思想。

比较组间差异与组内差异的大小，一般要用各自的方差来比较。方差的可加性是方差分析的基本理论依据，也就是方差的可分解性。作为一种统计方法，方差分析把实验数据的总变异分解为若干个不同来源的分量。不同来源的变异只有可加时，才能保证总变异分解的可能。具体来说，就是将总平方和分解为几个不同来源的平方和。

（四）各变异的原因及分解(www.xing528.com)

对于实验中的任何一个数据Xij，它与总平均数的离差等于Xij与该组平均数的离差加上该组平均数与总平均数的离差（Xj-Xt）之和，即：

式中：Xij为各实验数据（i表示样本内数据，i=1，2，3，…，n；j表示样本个数，j=1，2，…，K）；为总体平均数；为第j个样本的平均数。

如果对公式（8-1）求离差平方和，也就是求K组数据中的每个数据与总平均数的离差平方和，则有：

其中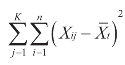：称为总平方和，是所有数据与总平均数的离差平方之和，用SSt表示。称为组内平方和，是每个样本内各个数据与本组平均数离差平方之和，用SSw表示。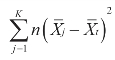称为组间平方和，是指各个样本平均数与总平均数离差平方和，用SSb表示。那么方差分析即是把总平方和分解为组间平方和与组内平方和。用式子表示为：

方差分析中，组间变异与组内变异的比较必须用各自的均方，不能直接比较各自的平方和。因为平方和的大小与项数（即K或n有关），应将项数的影响去掉，求其均方，因此必须除以各自的自由度。

MSb表示组间方差，一般称作组间均方，指实验处理的均方。dfb为组间的自由度。MSw表示组内方差或称组内均方，指随机误差的均方。dfw为组内的自由度。

由于检验两个方差之间的差异用F检验，因此比较MSb与MSw也要用F检验。由于我们在方差分析中关心的是组间均方是否显著大于组内均方，如果组间均方小于组内均方，就无须检验。所以在求F值时，总是把组间的均方放在分子的位置上，采取单侧检验，即：

按组间自由度和组内自由度查F分布表，找到Fa，如果F＜Fa，则认为各平均数之间差异不显著，说明总变异中由分组及不同实验处理造成的变异不大，其差异是由随机因素造成的。如果实际计算的F值较大，达到了一定显著性水平下的F分布理论值，则认为各组间这么大的差异完全由偶然因素产生是不可能的，表明数据的总变异基本是由不同的实验处理所造成的，因而我们有理由拒绝各组平均数相等的假设，认为各平均数并非来自同一总体，至少有一对平均数不相等。