双总体比例差异显著性检验结果

要检验两个独立样本的比例p1与p2有无显著差异，即检验两个样本是否抽自相同的总体，就要对两个样本的比例的差异进行显著性检验。检验时统计量U的计算公式如下：

当n1≠n2时为：

当n1=n2时，公式为：

式中：p1、p2分别为两个样本的比例；

　　　n1、n2分别为两个样本的容量；

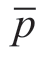　　　为两个样本比例的加权平均数。计算公式为：

式（7-9）的分母和式（7-10）的分母为比例的标准误，用SEp表示。

请看具体的例子。

例：为了调查男、女生对中学办重点班的意见，现从男生中随机抽取80人，赞成办重点班的有52人；抽取女生70人，赞成办重点班的有34人，问男、女生对办重点班的意见是否有显著差异？

题析：男生和女生对中学办重点班的态度是相互独立的，他们的态度可以用人数的比例反映出来。因此，这是属于检验两个样本比例差异是否显著的问题。

检验的步骤为：

1.建立虚无假设H0：π1=π2

2.计算统计量U的值

把各数值代入（7-9）得：(www.xing528.com)

3.取α=0.05，则U0.05=1.96

4.比较，做出判断

因为U=1.97＞U0.05=1.96，U的值落入拒绝区域，因而拒绝H0。即我们有95%的把握认为，中学男、女学生对办重点班的态度有显著差异。

例：为了了解甲、乙两县初中教师学历的达标情况，现从甲、乙两县的初中教师中随机抽取各150人的样本。甲县教师学历达标的有103人，乙县有84人，问甲、乙两县初中教师学历的达标率是否有差异？

检验的步骤为：

1.建立虚无假设H0：π1=π2

2.计算U的值

3.取α=0.05，则U0.05=1.96

4.比较，做出判断

因为U=2.32＞U0.05=1.96，U值落入拒绝区域，因而拒绝H0。即在α=0.05的水平上，甲、乙两县初中教师的学历达标率差异显著。

若本例取显著性水平α=0.01，U0.01=2.58时，则计算出来的统计量U=2.32＜U0.01=2.58，这时，U落入接受区域，因此我们必须接受H0，即接受甲、乙两县教师达标率没有显著差异的结论，这与上面的结论恰恰相反。

为什么同一个问题会得到截然相反的结论呢？这是因为显著性水平α的取值不同。显著性水平α的值越小，差异由抽样误差所造成的概率越小，要求也就越高，因而接受区域也就越长，计算出来的统计量U的值也越容易落入接受区域。由此可见，由于显著性水平α的取值不同，同一个问题有时会得到完全相反的结论。