U检验在教育与心理统计学中的应用

这是已知总体标准差σ，或总体标准差σ未知，但样本为大样本（n≥30）的平均数差异的显著性检验。因为大样本的平均数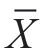的抽样分布服从正态分布，因而采用统计量U（或Z）。

（一）单总体的U检验

单总体的U检验，是检验样本是否来自原来的总体，也就是检验样本平均数与总体平均数μ0的差异的显著性。对于一个已知的样本平均数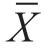，我们总是希望它能与一个平均数为μ0的总体在本质上一致。但这种一致性的程度如何，在没有经过检验之前，我们是不能下结论的，因此必须对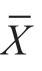与μ0之间的差异进行显著性检验。若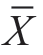与μ0的差异是由随机误差造成的，就说明它们之间无显著差异；否则，就差异显著。单总体U检验的虚无假设H0为：μ＝μ0（双尾）。统计量U的计算公式为：

式中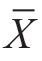，为样本平均数；

μ0为已知的总体平均数；

σ为总体标准差；

n为样本容量。

由公式（7-1）计算出来的统计量U的值，也就是标准正态分布表中的Z值。

请看具体的例子。

例：某县初中统考化学的平均成绩为76.3分，标准差为7.2分。甲校85名学生的化学平均成绩为80.5分。问该校85名学生的化学成绩与全县的平均成绩是否一致？

题析：全县考生的化学成绩是总体，甲校85名考生的化学成绩只是这个总体中的一个样本。本例的目的是检验样本平均数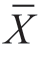=80.5与总体平均数μ0=76.3之间的差异是否显著的问题，属于单总体的U检验。

检验步骤如下：

1.建立虚无假设H0：μ=μ0（或μ＝76.3）

2.计算统计量U

例中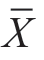，=80.5，μ0=76.3，σ=7.2，n=85。

将以上数据代入公式（7-1）得：

3.确定显著性水平α的值

取α=0.01，查表得U0.01=2.58。

4.比较，做出判断(www.xing528.com)

本题计算得到的统计量U=5.38＞Uα=2.58，即统计量U落入拒绝区域，因而拒绝虚无假设H0。因此，我们可以说，该校85名学生统考的化学成绩与全县的平均成绩在α=0.01的水平上，差异是显著的。

（二）双总体的U检验

双总体的U检验是检验两个样本各自所代表的总体平均数μ1和μ2的差异是否显著，即两个样本是否来自同一个总体。

双总体U检验统计量U的基本计算公式为：

式中，分别为两个样本的平均数；

　　　n1、n2分别为两个样本的容量；

　　　σ1、σ2分别为两个总体的标准差。

例：为了评价甲、乙两校学生的数学水平，随机从甲校中抽取50名学生，乙校中抽取60名学生进行数学测验。其结果为，甲校50名学生的平均分为72分，标准差为10.5分；乙校60名学生的平均分为70分，标准差为9.4分。请问两校学生数学成绩有无显著差异？（α=0.10）

题析：本题是检验两个大样本所代表的总体平均数是否有显著差异的问题，属于双总体的U检验问题。由公式（7-2）可知，要计算统计量U的值，必须知道两个总体的标准差。而本题中两个总体的标准差σ1和σ2未知，只知道样本的标准差S1和S2，因为是大样本，所以我们可以用S代替σ。

检验的步骤如下：

1.建立虚无假设H0：μ1=μ2。

2.计算统计量U的值。

已知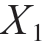：=72，X2=70，S1=10.5，S2=9.4，n1=50，n2=60。

代入公式（7-2）得：

3.题中已知α=0.10，查表得临界值 U0.10=1.64。

4.比较，做出判断。

统计量U=1.04＜Uα=1.64，表明统计量U落入接受区域，因而接受H0。故我们可以得出结论：在α=0.10的水平上，甲、乙两校学生的数学成绩无显著差异。

上述U检验，是总体的标准差σ已知或总体标准差未知但样本是大样本的平均数差异的显著性检验问题。对于总体标准差σ未知，又是小样本的情形，必须借助统计量t进行检验。