【摘要】：差异是否显著，或者差异的显著性如何，是用随机误差所产生的概率的大小来测定的。差异由随机误差造成的概率的大小，称为显著性水平，通常用α表示。随机误差产生的概率即显著性水平究竟多大才算较大，多少才算较小呢？取α=0.05，说明显著性水平确定在0.05这个水平上。α=0.05这个概率，实际上是指我们判断发生错误的可能性是5%，即差异由随机误差产生的可能性在100次事件中发生5次。
差异是否显著，或者差异的显著性如何，是用随机误差所产生的概率的大小来测定的。若样本统计量（如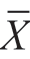
）与总体参数（如μ）之间的差异由随机误差造成的概率较大，我们就认为差异不显著；若这种差异由随机误差造成的概率很小，我们就认为差异显著。差异由随机误差造成的概率的大小，称为显著性水平，通常用α表示。随机误差产生的概率即显著性水平究竟多大才算较大，多少才算较小呢？这要视具体问题的具体要求而定。一般在评价教育现象时，α的值通常取0.10、0.05和0.01等几个值。取α=0.05，说明显著性水平确定在0.05这个水平上。若检验的结果α＞0.05，则说明差异不显著（在α=0.05这个水平上）。若α≤0.05，就说明差异显著。α=0.05这个概率，实际上是指我们判断发生错误的可能性是5%，即差异由随机误差产生的可能性在100次事件中发生5次。例如，我们要评价一所学校学生的数学水平，可以从这所学校中随机抽取30名学生进行测验，设测验结果为
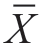=73分，若全县学生的平均成绩是μ=75分，我们可以通过差异显著性检验来判定μ与
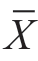之间的2分之差是由什么原因造成的。若取α=0.01，检验结果是α＞0.01，那么可以说在α=0.01这个水平上，μ与
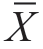之间的差异不显著，也就是说，μ与
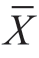之间的2分之差由随机误差产生的概率大于1%。显著性水平α是个较为抽象的概念，以后再通过例子加以说明。(www.xing528.com)
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
