教育与心理统计学：总体平均数的区间估计

我们知道抽取样本，计算出样本的各种统计量，并不是统计工作的最终目的。我们总是希望用样本统计量去估计总体的参数。这一节我们研究如何用样本的平均数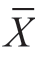去估计总体参数μ。

（一）样本平均数的标准误

用样本平均数去估计总体平均数常常会产生误差。在做估计之前，我们首先要知道这种误差究竟有多大。这就是样本平均数的标准误。

所谓样本平均数的标准误，就是样本平均数抽样分布的标准差。用符号表示。这个定义较难理解，我们举例来说明。在一个总体中，我们可以抽取n个样本，每一个样本都有一个平均数。设n个样本的平均数分别为，这n个平均数也有一个标准差，这个标准差就称为标准误，标准误的本质仍然是标准差。样本平均数标准误的基本计算公式是：

式中，表示样本平均数的标准误；

　　　σ表示总体标准差；

　　　n表示样本容量。

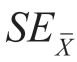越小，样本平均数与总体平均数越接近，样本对总体越有代表性，用样本平均数去估计总体平均数的可靠性越高，反之，越低。

我们用公式（6-20）计算平均数标准误，需知道总体标准差σ的值。但总体是估计的对象，σ的值往往是不知道的。在这种情况下，我们只能用样本标准差S去代替σ。当样本为大样本（n≥30）时，样本标准差S与总体标准差相差不会太大，因而大样本平均数的标准误的计算公式可改写为：

式中，S表示样本标准差。

（二）总体平均数区间估计的方法

1.大样本情况下总体平均数的估计

有了样本平均数的标准误之后，我们便大概知道样本平均数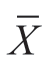与总体平均数μ的差异了。这时，我们便可以以样本平均数为中心，推算总体平均数离开样本平均数这个中心点的距离。因为是估计，所以就有估计的把握（即可能性）有多大的问题，这种可能性用概率来表示，称为置信系数或置信度。

由于区间估计的统计学原理较难懂，这里省略。下面只写出总体平均数区间估计的通用公式和几个较常用的置信度所对应的总体平均数的置信区间的计算公式。

置信度为90%的置信区间为：

置信度为95%的置信区间为：

置信度为99%的置信区间为：

公式（6-22）可以理解为总体平均数μ落在样本平均数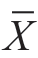-1.64SEX和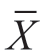+1.64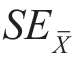之间的可能性为90%。不等号左边的值称为置信下限，不等号右边的值称为置信上限。其余公式也大致如此理解。

请看具体例子。

例：从某市随机抽取初一学生50名，测得身高的平均数为149厘米，标准差为8厘米，问该市初一学生的平均身高大约是多少？已知置信系数为95%。

本例样本容量n=50＞30，属于大样本情况下总体平均数的区间估计。样本平均数的标准误为：

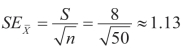(www.xing528.com)

由公式（6-23）可知总体平均数μ的置信区间为：

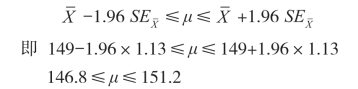
故该市初一学生平均身高置信度为95%的置信区间为［146.8，151.2］。

2.小样本情况下总体平均数的估计

用样本平均数估计总体平均数需知道标准误。标准误的基本计算公式是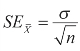，但是，σ在一般情况下是不可能知道的，这时必须用S代替σ。在大样本（n≥30）的情况下，S与σ相差不大，可以直接用S代替σ；而在小样本（n＜30）的情况下，用S代替σ，求得的标准误一般偏小。为了克服这种将低估的倾向，通常用（n-1）代替n，故小样本求标准误的计算公式为：

这时，样本平均数的抽样分布已不再服从正态分布，而是服从一种新的分布——t分布。t分布也是一种样本统计量的抽样分布。其计算分式为：

我们称这样的t分布为服从自由度为n-1的t分布。自由度用符号df表示，即df=n-1。不同的自由度有不同的t分布。这里需要对自由度做解释。

所谓自由度是指样本中能独立地自由变动的变量个数。例如，有5个变量分别是X1、X2、X3、X4、X5，当没有任何限制时，这5个变量都可自由变动，即自由度为5。但当限定它们的平均数为一个固定值时，其中4个变量任意取值之后，最后一个变量就随之确定了，因而只有4个变量可以自由变动。即自由度df=4。若限制条件增加一个，则自由度便减少一个。自由度并不都等于n-1，它是随着限制条件的不同而不同的。

t分布是一种理论分布，其分布形态和特点与正态分布基本一样。所不同的是，t分布曲线的横轴是t轴，正态分布曲线的横轴是Z轴；t分布曲线的形态受自由度df的影响，而正态分布受标准差σ的制约。统计学家已经为我们编制了不同自由度t分布的临界值表（见附表3）。在t值表中，左边第一列的df表示不同的自由度；上面第一行P（2）、第二行P（1）表示不同的显著性水平。显著性水平用符号α表示。P（2）表示将α的值分置于t分布曲线的左、右两侧，P（1）表示将α值置于t分布曲线的一侧。表中的数字表示某一自由度df和某一显著性水平α所对应的t的临界值，它一般用符号tα（df）表示。t下面的df表示自由度，α表示显著性水平。如t0.05（10）表示自由度为10，显著性水平为0.05的t的临界值，这个临界值便是自由度df=10，显著性水平P（2）=0.05所对应的行和列交叉处的那个值。从表中可查出t0.05（10）=2.228。再如t0.01（7），查附表3可知其值为3.499。其余也知此。

有了t值表以后，我们便可对小样本情况下的总体平均数进行估计了。计算置信区间的公式为：

在式中，α的值等于1减去置信系数。

请看具体的例子。

例：为了调查某校初三学生的英语水平，现从中随机抽取15名学生参加测验，得平均成绩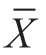=78分，标准差S=5.9分。问该校初三学生英语平均成绩置信度分别为90%、95%和99%的置信区间是多少？

题析：因样本的容量n=15，故这是属于小样本的总体平均数的估计问题，需利用t值表。

样本的标准误为：

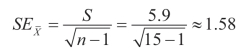
查t值表可知，t0.10（14）=1.761。于是，置信度为90%的μ的置信区间为：

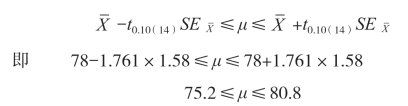
查t值表可得：t0.05（14）=2.145，t0.01（14）=2.977。

同理可得，置信度为95%的μ的置信区间为：

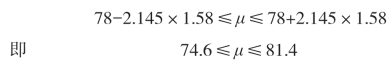
置信度为99%的μ的置信区间为：

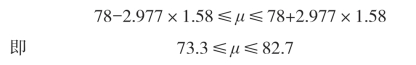
从上例可以看出，置信度越高，置信区间越长；反之，越短。这是因为置信度就是对估计的要求，对估计的要求越高，越要拉大估计区间。