正态曲线下面积的应用

（一）求某些分数区间的百分数或人数

在分析测验结果的时候，我们常常想了解处于某些分数区间的考生人数或百分数，这就需要利用正态分布表。因为在一般情况下，考生的成绩近似于正态分布。下面通过例子加以说明。

例：某班50名学生某次数学测验的成绩基本服从正态分布，平均成绩为72分，标准差为10分。利用正态分布曲线下的面积求60分以上、70—80分、80—90分各有多少人？

由于学生的成绩服从正态分布，因此，我们可以利用正态分布曲线下的面积比例来求各分数段的人数，而不必用试卷做统计。因为正态分布曲线的横轴为Z值，所以，我们必须先将原始分数化成标准分，然后用总人数乘以面积比例，便可求出各分数区间的人数。

本题的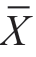=72，S=10，则：

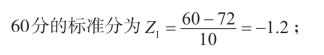
查附表2。

当Z1=-1.2时，P1=0.1151；

Z2=-0.2时，P2=0.4207；

Z3=0.8时，P3=0.7881；

Z4=1.8时，P4=0.96407。

Z1=-1.2是60分所对应的标准分，P1=0.1151是Z1=-1.2以下面积的比例，而正态分布曲线下的总面积为1，则60分以上的人数比例应为：1-0.1151=0.8849。同理70—80分的人数比例为P3-P2=0.7881-0.4207=0.3674。80—90分的人数比例为P4-P3=0.96407-0.7881=0.17597。

最后我们把总人数乘以各分数区间的人数比例即可得到各分数段的人数：

60分以上：50×0.8849≈44（人）；

70—80分：50×0.3674≈18（人）；

80—90分：50×0.17597≈9（人）。

（二）求某一团体中特定比例的分数界限

例：已知某次测验分数服从正态分布，其平均分为80分，标准差为10分。求中间70%学生分数的区间。

题析：因为正态分布是完全对称的，包含中间的70%的比例，就是标准正态曲线对称轴（Z=0）左右各占35%的面积比例。这就是由面积比例反求Z值的问题。由于附表2中面积的值是某一Z值左侧曲线下的面积比例，若要求平均数下35%的面积所对应的Z值，查表时应查面积比例为0.5-0.35=0.15所对应的Z值；同理，要求平均数以上35%面积比例所对应的Z值，查表时应查0.5+0.35=0.85的面积比例所对应的Z值。但由于正态分布曲线的完全对称性，只要求出其中一个Z值，另一个Z值也就迎刃而解（这两个Z值绝对值相等，符号相反）。如图6-4所示。用插值法计算。

图6-4　例题分析图

查附表2中的面积部分，我们找不到面积比例为0.85这个值，但可以找到与它最接近的两个数：0.8485和0.8508。这两个面积比例所对应的Z值分别为1.03和1.04。

由上分析可知，P=0.85，P1=0.8485，P2=0.8508，Z1=1.03，Z2=1.04。

由插值公式（6-19）可得：(www.xing528.com)

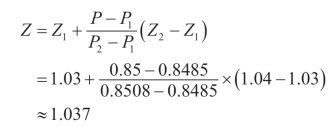
那么，对称轴以下35%的面积比例所对应的Z值应为-1.037。

现在，用标准分反求原始分数。由公式：

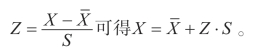
于是，当Z=-1.037时，X=80-1.037×10≈70

当Z=1.037时，X=80+1.037×10≈90。

故包含中间70%面积比例的成绩应在70至90之间。

（三）进行能力分组或评定成绩

例：某年级共有250人，假定能力测验的结果符合正态分布。现按能力分为4组，问各组的人数应是多少？

题析：这是利用正态分布曲线下面积进行能力分组的问题。从理论上说，正态分布曲线的左、右两条尾巴向左、右方向无限伸展，因而Z的值也应从-∞到+∞。但是，当Z＜-4.00或Z＞+4.00时，其左、右两条尾巴与横轴所包含的面积几乎可以忽略不计。因此一般情况下，横轴的Z值取-4σ至+4σ之间8个单位的距离。现要将其分成4等份，则每份应占的距离为8σ÷4＝2σ。如图6-5所示。

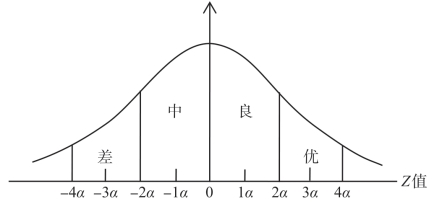
图6-5　能力等级分布图

现在，只要求出优、良、中、差4个能力等级所占的比例，便可知道各组的人数。由正态分布曲线的对称关系可知，优与差、良与中的比例和人数都应相等，因此，只要求出优与良或中与差任意两组的比例就行了。

优等组的面积比例所对应的Z值是从2.00到4.00。

当Z=2.00时，P=0.97725；

当Z=4.00时，P=0.946833。

故优等和差等级的人数比例为：

0.946833-0.97725≈0.0227

良等级的面积比例所对应的Z值为0到2.00之间。因为Z=2.00时，P=0.97725，所以，良等组和中等组的面积比例应为0.97725-0.5=0.47725。

因此，各组的人数分别为：

优等、差等的人数各为：0.0227×250=6（人）。

良等、中等组的人数各为0.47725×250=119（人）。

利用正态分布曲线下的面积，还可以分析试题的难度。