教育与心理统计学-排列与组合方法及种类，包括计算方法与示例

（一）排列

把n个不同的元素按一定的顺序排成一列，叫作n个不同元素的全排列。所有不同全排列的种数，用nPn表示，也可用Pn或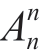表示。

这个公式的计算可做如下说明。

第一个位置，可以从n个元素中任取一个来排，共有n种方法。

第二个位置，在剩下的n-1个元素中任取一个来排，共有n-1种方法。

第三个位置，在剩下的n-2个元素中任取一个来排，共有n-2种方法。

这样继续取，直到最后第n个位置，只剩下一个元素，只有一种方法。

例如3个字母，每次取3个，排列方法为：3P3=3！=3×2×1=6。

若此3个字母为a、b、c，则其排列方法有abc、acb、bac、bca、cab、cba六种。

与全排列不同的还有选排列。

选排列是指从n个不同元素中，每次取出r（r＜n）个不同的元素，按照一定的顺序排成一列，叫作从n个不同的元素中每次取r个不同元素的选排列。所有不同选排列的种数，用nPr来表示，也可用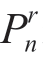表示。(www.xing528.com)

选排列和全排列的相同点是都要按照一定的顺序排列，其不同点是选排列每次只取部分元素。

计算选排列的公式为：

公式中n、r都是正整数，并且n＞r。

选排列与全排列在计算方法上基本相同。

计算选排列是当取到r位置时，应从其余n-（r-1）个元素中，任取一个元素来排列，共有n-（r-1）种方法（即n-r+1种方法）。

（二）组合

从n个元素中，每次任取r个元素，不论次序并成一组，叫作n个元素中，每次取r个元素的组合。不同组合的种数，用nCr表示，也可用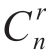表示。

例如，从A、B、C三个不同元素中每次取两个的组合有几种？

由于组合没有顺序的要求，因而从A、B、C三个不同元素中每次取两个的组合，结果只有AB、BC、CA三种。

由此可以看出，从三个不同元素中每次取出两个，不论次序并为一组，即组合的种数为3C2；若把每一组合里的两个元素进行全排列，则共有2P2种排法，因而可得出以下公式：