教育与心理统计学：三位学生的标准分数对比

（一）标准分数的概念

标准分数是原始分数与平均数的离差除以标准差所得的商。用符号Z或（U）表示，因而也称为Z分数。

（二）标准分数的计算方法

由定义可知，标准分数的计算公式为：

式中，Z为标准分数；X为某原始分数；S为标准差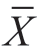；为平均数。

标准分数没有实际单位，它不仅能表示原始数据在一组数据分布中的地位，在不同分布的各原始数据之间进行比较，而且还可以将两个不同单位的数据转化为标准分进行比较。

例：某班语文测验的平均分为80分，标准差为7分。现有甲生得75分，乙生得94分，丙生得80分。求三位学生的标准分数。

把题中各数值代入公式（4-9）得：(www.xing528.com)

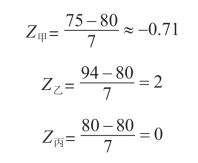
从例中可以看出，标准分数有正数、负数和零。原始分数等于平均数，其标准分数等于零；原始分数大于平均数，其标准分数为正数；原始分数小于平均数，其标准分数为负数。标准分数表示原始分数与平均数之间的地位关系，因此，标准分数是一种地位量数。标准分数的绝对值，说明了该原始分数与平均数的距离，绝对值越大，距离越远；反之，距离越近。

由于标准分数是一种没有单位的纯量数，因此，它具有可比性和可加性。而原始分数带有原来的测量单位，因而不具有可比性和可加性。目前在教学或教育评估中，用原始分数来比较多学科的总成绩，是不合理、不科学的，而必须用标准分数。

例：甲、乙两名学生五科考试成绩如下，试分析哪名学生成绩好一些。

表4-3　甲、乙两考生总成绩标准分数计算表

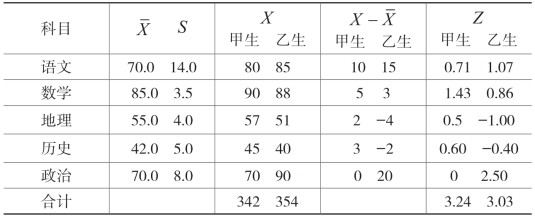
如表4-3所示，甲生的标准分数Z=3.24，而乙生的标准分数Z=3.03。从标准分数看，甲生成绩优于乙生。而从原始分数看，甲生成绩差于乙生。为什么会出现两个截然相反的结论呢？这是因为，不同考试科目试题的难易程度不同，分数的价值也不可能一样，如例中的数学和历史两科，可能由于数学试题较容易，而历史试题较难，两科平均分数相差悬殊，因而其分数的价值不一样。可以说，同样1分，历史分数的价值远远大于数学分数的价值。原始分数忽视了不同科目分数的价值不同这一重要信息，因而，用原始分数比较多学科的总成绩是不合理、不科学的。因此，在分析学生成绩时，应把原始分数转化为标准分数，再进行比较才合理、可靠。