《教育与心理统计学》中的方法：众数与皮尔逊近似法

众数是指一组数据中出现次数最多的数值，用符号Mo表示。如有一组数据为2、5、7、2、2、5，在这组数据中，2出现的次数最多，故Mo=2。由于众数是一组数据中出现次数最多的数值，它带有普遍性，因此，可以用来说明这组数据的一般水平。

众数的计算方法：

（一）用观察法求众数。根据众数的定义，只要我们把数据进行整理，出现次数最多的数据便是众数。如上例，2出现三次，最多，所以2便是众数。当数据已归类分组，制成次数分布表以后，众数便落入次数最多的那一组内。但是，在这一组里的无穷多个数中，究竟哪一个数为众数呢？如果只做粗略的估计，那么这一组的组中值便为众数。如表3-2中，35—39这一组的次数最多，其组中值37便可作为粗略的众数。

（二）用皮尔逊近似法求众数。英国统计学家皮尔逊研究发现，次数分布完全对称的数据资料，其算术平均数、中位数、众数三者必然重合。当次数分布不完全对称时，平均数、中位数和众数三者也有一种近似的稳定关系，这种关系可用式子（X-Mo）∶（X-Md）=3∶1表示，即：

这就是皮尔逊近似法求众数的公式。

以表3-2的数据为例，用皮尔逊法求众数。

将Md=36.6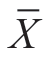，=36.1代入公式（3-4）得：

Mo=3Md-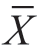=3×36.6-2×36.1=37.6

（三）用插入法求众数。为了更精确地求取众数，我们也可以采用插入法。其计算公式为：(www.xing528.com)

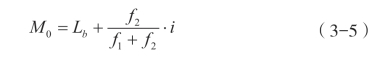
式中　Lb为众数所在组的下限；

　　　f2为众数组上限相邻一组的次数；

　　　f1为众数组下限相邻一组的次数；

　　　i为组距。

以表3-2的资料为例求众数Mo。

题中，Lb=35，f2=24，f1=21，i=5，则众数：

从以上计算结果可以看出，用插入法计算众数与用组中值或用皮尔逊近似法计算众数都略有出入，其中以插入法最为精确，皮尔逊法次之，用组中值估计众数最为粗略。