中位数是指一组数据按大小顺序排列,居中间位置的那个数据的数值。用符号Md或Mdn表示。中位数也是一种集中量数,它可以用来表示一组数据的一般水平。
当数据的个数是奇数时,中位数就是居正中的那一个量数。如一组数据为:
3,5,4,1,7,6,3。
求这组数据的中位数,先要将这组数据按大小顺序排列:1,3,3,4,5,6,7。因为数据的个数是7,因此,居中间的是第四个数据,这个数据的值为4,故Md=4。
当数据的个数为偶数时,位于中间的已经不是一个数而是两个数了。在这种情况下,中位数为位于中间的两个数的平均数。
如一组已排序的数据:2,5,7,8,10,11。按照中位数的定义,Mdn应是处于![]() =3.5位置上的那个数。但是,第3.5位上的数是不存在的,这时中位数应是位于第3位和第4位的两个数据的平均数,故Md=
=3.5位置上的那个数。但是,第3.5位上的数是不存在的,这时中位数应是位于第3位和第4位的两个数据的平均数,故Md=![]() =7.5。一旦数据已经分组,尽管我们同样可以知道中位数的位置,但是,对应这个位置的那个数据的值,我们却无法知道,这时需用另一种方法来求中位数,计算公式为:
=7.5。一旦数据已经分组,尽管我们同样可以知道中位数的位置,但是,对应这个位置的那个数据的值,我们却无法知道,这时需用另一种方法来求中位数,计算公式为:
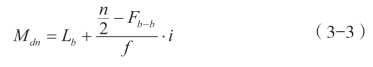
式中 Lb表示中位数所在组的精确下限;
Fb为中位数所在组以下的累积次数;
n为总次数; i为组距;
f为中位数所在组的次数。(https://www.xing528.com)
下面通过例子加以说明。
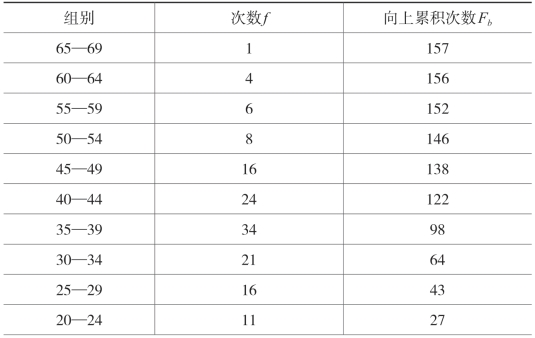
例 求表3-2中数据的中位数。
表3-2 对分组数据求中位数示例
(续表)

计算步骤:(1)求![]() ,因为n=157,所以
,因为n=157,所以![]() =78.5,也就是说,中位数落在第79位数据的身上;(2)确定中位数所在组。从表中可以看出,数据积累至30—34这一组时,累积次数已达到64次,而35—39这一组有34个数据,因此,可以确定中位数落入35—39这一组内;(3)确定中位数所在组的精确下限,即Lb,本例Lb=34.5;(4)确定中位数所在组以下的累积次数,即Fb,Fb=64;(5)确定中位数所在组的次数f,f=34;(6)确定组距i,i=5。
=78.5,也就是说,中位数落在第79位数据的身上;(2)确定中位数所在组。从表中可以看出,数据积累至30—34这一组时,累积次数已达到64次,而35—39这一组有34个数据,因此,可以确定中位数落入35—39这一组内;(3)确定中位数所在组的精确下限,即Lb,本例Lb=34.5;(4)确定中位数所在组以下的累积次数,即Fb,Fb=64;(5)确定中位数所在组的次数f,f=34;(6)确定组距i,i=5。
综上所述,本例的Lb=34.5,![]() =78.5,Fb=64,f=34,i=5,代入公式(3-3)得:
=78.5,Fb=64,f=34,i=5,代入公式(3-3)得:
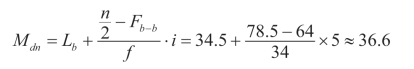
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




