简单次数分布表：教育心理统计学

让我们用例子来说明次数分布表的编制步骤。

下面是某校初二（1）班50名学生的几何期末考试成绩：

现在，我们要把这些杂乱无章的数据变成按一定的规则排列的数据，也就是编制次数分布表。一般步骤如下：

（1）求全距。全距也称两极差，它是全部数据中最大值与最小值之差，用符号R表示。

在本例中，R=98-40=58。

（2）定组数。定组数就是在分数统计中把大量的数据划分为一定的分数档。一群数据究竟分为多少组为宜，统计学中没有严格规定，原则上便于使用即可。分组过多，达不到化繁为简的目的；分组过少，容易产生丢失信息的现象，造成失真。一般来说，分10～15组为宜。本题中，R=58，拟分为12组。

（3）求组距。组距是指每一组数据的间距。它是全距除以组数所得的商，用i表示。本例i==4.8。当i值不是整数时，为了便于计算，一般要取整数值。本题中，i=5。

（4）确定组限。组限就是一组分数的起点值和终点值。起点值称为下限，终点值称为上限。在统计学中，组限的写法多种多样，为了便于掌握，此题的组限可写为95—100，90—95，85—90……但必须注意，这种写法只是一种表述形式，而不是实际组限，实际组限应是94.5—99.5，89.5—94.5，84.5—89.5……

（5）求组中值。组中值是每组数据分布正中位置的点值，它是每组数据的代表值，用Xc表示。它的求法是该组数据的精确下限与精确上限之和的一半，即Xc=(www.xing528.com)

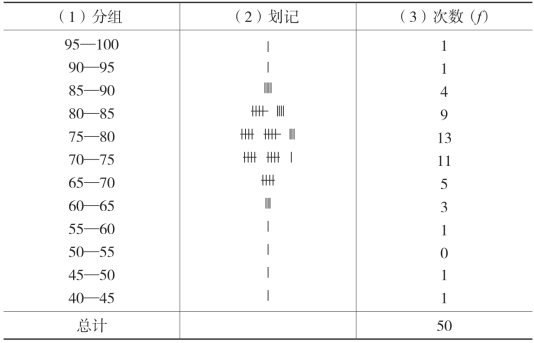
（6）归组划记。确定组限以后，我们就可以将每个数据逐一登记，归入所属的组内。登记时一般采用画线记数（“”或“正”）。然后将各组数据的个数记入次数（f）栏中。表2-1的第一栏和第三栏就构成了本题的次数分布表。

表2-1　某校初二（1）班期末几何成绩划记登记表

（一）累积次数分布表

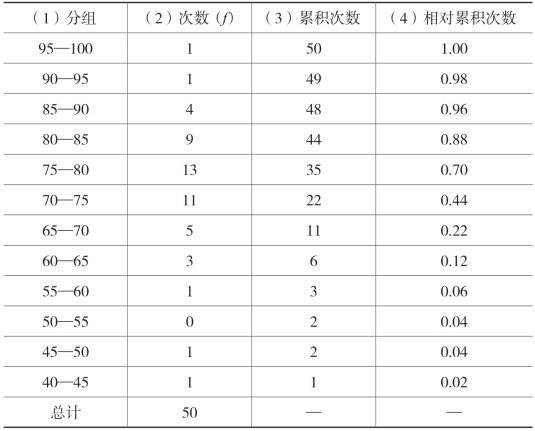
累积次数分布表是指在次数分布表的基础上，将各组的次数自下而上或自上而下依次累加所形成的表。自下而上的累加称为向上累积；自上而下的累加称为向下累积。累积的最后次数应等于总次数。表2-2中的第一栏和第三栏便构成了本题的累积次数分布表。

表2-2　某校初二1班期末几何成绩相对累积次数表（向上累积）

（二）相对累积次数分布表

相对累积次数分布表，是在累积次数表的基础上将各组的次数除以总次数所得的数，亦即频率。表2-2中的第一和第四栏便构成了相对累积次数分布表。