费尔马大定理：数学界的未解之谜

我们知道，用长分别为3，4，5个单位的木条或绳子能组成一个直角三角形。在几千年以前，古埃及的建筑师们就已经懂得这个原理，并且用它来建造埃及法老们的陵墓——金字塔，给人类留下了光辉灿烂的文化遗产。工智能

除了3，4，5外，还有无数个正整数a，b，c能作为直角三角形的边长。也就是说满足关系式

a2＋b2＝c2。

这个关系式就是有名的勾股定理。我们把满足勾股定理的三个正整数称为是一组整数勾股数。

现在的问题是，怎样找出一个求所有整数勾股数的公式来?

首先我们明显地知道，如果a，b，c是一组整数勾股数，那么对任意的正整数p，pa，pb，pc也是一组整数勾股数。因此下面我们只讨论a，b，c没有整公约数的简单情况。

如果a，b，c是一组整勾股数，容易证明在a，b中一定有一个是奇数，一个是偶数。

因为如果a，b均为偶数，则a2＋b2也是偶数，因此c2是偶数，进而c也为偶数。这不符合我们简单情况的假设(没有整公约数)。

如果a，b均为奇数，设a＝2m＋1，b＝2n＋1，

则a2＋b2＝(2m＋1)2＋(2n＋1)2＝4(m2＋m＋n2＋n)＋2，这说明c应该是一个偶数，但这时c2应该是4的整数倍，而不会等于4(m2＋m＋n2＋n)＋2形式的数。因此a，b都是奇数的假设也不成立。

所以a，b中必是一奇一偶，进而知道c必定是一个奇数。

我们假定a是奇数，b是偶数，把等式

a2＋b2＝c2

变形为

a2＝c2－b2＝(c＋b)(c－b)。

可以证明c＋b，c－b是互质的(没有非1的公约数)。

如果它们有一个非1的质公约数，设为p，那么p也应该是(www.xing528.com)

(c＋b)＋(c－b)＝2c，

(c＋b)－(c－b)＝2b，

(c＋b)·(c－b)＝a2

三者的公约数。因为a是奇数，这个公约数不是2，那么就得出b，c，a有另外的公约数的矛盾。因此，c＋b，c－b是互质的。再由这两个互质数的积是一个完全平方数，因此c＋b，c－b都分别是一个完全平方数，我们设

c＋b＝m2，c－b＝n2，

把两式联立，解出c＝。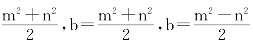

这样我们就得到简单的整数勾股数的一般表达式

其中m，n是互质的奇数，且m＞n。对于任给一对满足此条件的m，n的值，我们都可以由公式求出一组简单的整数勾股数。

上面讨论的a，b，c我们规定都是正整数，如果允许取负整数，在所求得的任一组勾股数中，三个数无论取什么符号，等式a2＋b2＝c2始终成立。

对数学的研究，我们总是沿着特殊到一般的道路前进的，解决了这类问题之后，同学们一定会问：能否找到三个正整数a，b，c，使它们满足关系式a3＋b3＝c3?

更一般地，对n＝3，4，5，…，能否找到正整数a，b，c，使它们满足关系式an＋bn＝cn?对此，至今人们认为结论是否定的，这就是著名的费尔马大定理。它的完整叙述是：

当n是大于2的正整数时，方程xn＋yn＝zn没有整数解。

费尔马并不是一个职业的数学家，他是学法律的，只是业余从事数学研究，但他是一个很了不起的数学天才，在数学上作出了很多的贡献。另外他思路敏捷，善于猜想，他博览群书，并且经常把他的心得写在读过的著作的边上。上面这个问题(xn＋yn＝zn，整数n＞2，没有整数解)也是刁藩都的著作中的一个问题，费尔马在读了这本书后，在这一页的边上写着：“我已经找到了这个命题的真正奇妙的证明，但是这里地方太小，写不下了。”

遗憾的是在他逝世之后，人们查遍他的所有遗物也未能找到这个“奇妙的证明”。

费尔马的后继者们，包括欧拉等著名的数学家搅尽了脑汁，也只证明了对n的一些数值，费尔马大定理成立。对于一般情况确是一个世界难题。究竟原来费尔马是否已找到了那个奇妙的证明，或者是他找到的证明有所失误，人们至今不得而知，因此费尔马大定理经历了很长的时间，仍是一个猜想。但据美国《纽约时报》报道，1993年6月24日美国普林顿大学教授、英国数学家安德鲁·外尔斯宣布：费尔马大定理已得到证明(详见湖北与武汉数学会及华中师范大学数学系合编《数学通讯》1993年第10期，或与湖北与武汉数学会副理事长齐民友教授联系)。