数学领域的未解之谜-皇冠上的明珠

一看到这个标题，读者们就会猜到我在这里要介绍的是有关哥德巴赫猜想的故事。

哥德巴赫先生是普鲁士派往俄国的一位公使。他对数学有浓厚兴趣和爱好。1742年6月7日，公使先生写信给当时正住在俄国的著名数学家欧拉说：“任何不小于6的偶数均可表示成两个奇素数之和”，“任何不小于9的奇数均可表示成三个奇素数之和”，并请欧拉帮他证明。

这两个结论是任何有小学数学水平的读者均能理解的。但却是包括欧拉在内的所有数学家至今尚未解决的难题。其中第二个结论可看成第一个结论的推论，因此我们讲的哥德巴赫猜想主要是指第一个。

猜想从一提出就引起各国数学家的关注，他们企图采用各种方法去证明它。

一部分人是去做验证的工作。验证不是证明，但如果能找到一个例外，就可以推翻这个猜想。尽管这些人花费了很多宝贵的时间，动用了包括电子计算机在内的计算工具，到目前为止所验证的一切数字，猜想都是正确的。

另一部分人是设法去证明猜想，为了证明，他们走过了漫长的道路，开辟了一个又一个新的研究领域，创造了许多的证明方法，但证明至今尚未结束。

这里值得一提的是我国数学家的功绩。我国的著名数学家华罗庚，王元，潘承洞，陈景润等在证明猜想的道路上付出了艰辛的努力，不断创造出领先于世界的证明方法和成果。目前这项世界纪录被陈景润所保持，他得到的结果是：任何一个大的偶数N，总可以找到两个奇素数p1，

p2或三个素数p1′，p2′，p3′，使得下面两个等式至少有一个成立：

N＝p1＋p2；N＝p1′＋p2′＋p3′。

这就是世人公认的“陈氏定理”。

不少数学爱好者企图用初等方法试探哥德巴赫猜想的证明，而且也不乏为此浪费了毕生精力的人。在此我想告诉读者的是，猜想的证明是极困难的，需要很多高深的数学知识。陈景润在中国科学院长期深造和研究，他的证明用了几年时间，光草稿纸就是几麻袋之多。最后他写出的定理证明长达200余页。由此可看出证明的难度。如果有人愿意为此继续奋斗的话，请你先把前人的证明看懂了再说，千万不要作不切实际的尝试。

“陈氏定理”离猜想仅差一步之遥，但从“陈氏定理”发表到现在20年过去了，还无人能跨越这一步，可见这猜想不愧为皇冠上的明珠。

哥德巴赫猜想讲的是关于整数的理论。整数是人们认识最早、研究得最多的数。在整数理论中除哥德巴赫猜想外还有很多著名的问题。

在公元前300年，著名数学家欧几里得证明了这样一个结论：“素数有无限个。”他的证明是用反证法，非常精彩。

证明:如果素数是有限的，有限个数可以全部取出来，并且能比较它们之间的大小。尽管可能费时很多，但从理论上这是办得到的。假如这有限个素数按从小到大顺序排列出来是：

2，3，5，7，…，p。

我们构造一个新的数

N＝2×3×5×7×…×p＋1

N显然大于p。由于p是最大的素数，所以N不是素数而是合数，那么N一定有素因数。它的素因数是怎么样的呢?

我们可以看出，2，3，5，7，…，p这些素数都不是N的素因数，因为当N被这些素数整除时，都余1．例如：＝3×5×7×…×p…余1，等等。这就说明N的素因数不在上面这些素数之中，也就是说除了2，3，5，7，…p这些素数外还有其他的素数，这与一开始假设素数只是这些有限个数是相矛盾的。矛盾产生的原因，是因为错误的假设，因此素数有无限个。

素数有无限个，能不能找出一个产生全体素数的公式出来呢?或者要求降低一些，能否找到一个公式，使它产生的都是素数呢?

1640年，法国的业余数学大师费尔马声言，他找到了这样的公式，那就是22n并且他验证了

这几个都是素数，于是他认为当n取4以上的数值时，公式仍然能产生素数。

遗憾的是他的这一猜想错了，在他提出这一猜想后100年，欧拉指出n＝5时所得的数不是素数，并计算出：

从这件事读者们可以学习到，光用验证特殊值的方法不是严格的证明，从特殊例子概括出一般的原理要特别小心，未经严格证明不能认为是正确的。

形如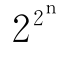＋1的数后人称为费尔马数，时至今日，当n≥5时人们还没有找到是素数的费尔马数。那么，是不是n≥5的一切费尔马数都不是素数呢?这又是一个新的猜想。(www.xing528.com)

尽管如此，人们对寻找出更大一些的素数仍有浓厚的兴趣，他们又研究了形如2n－1的数，这种数称为麦生数。

当n不是素数时，麦生数一定是合数。

1644年麦生验证了n＝2，3，5，7，13，17，19，31时，2n－1是素数。那么往下结果怎样?这一回可不能再犯费尔马的错误了。

美国的数学家在1903年公布了他的计算结果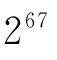，－1＝193707721×761838257287。后来有人问他“为证明这个问题您花了多少时间?”他的回答是“三年内的全部星期天。”

人们继续证明了n＝61，89，107，127时麦生数是素数，其中n＝127时，是一个39位的素数，这是法国数学家罗卡斯得到的。这是人用纸笔计算的最高记录。

电子计算机问世后，人们有可能得到更大的素数。1979年，美国学者证明出244497－1是一个长达13395位的素数。1983年又发现n＝86243时，麦生数也是素数。当然，新的更大素数还会继续被发现，但麦生素数到底有有限个还是无限个，人们至今还不能解答这道难题。

1742年，哥德巴赫写信给数学家欧拉，还提出了猜想：形如4n4＋1的任意数(n为自然数)，只有n＝1时才是素数，并请求欧拉解答。

欧拉在解答中是用配方法的(配方法是数学中的一个重要方法)。下面给出欧拉的解答。

解:4n4＋1＝(2n2)2＋4n2＋1－4n2

＝(2n2＝1)2－(2n)2

＝(2n2＋2n＋1)(2n2－2n＋1)

当n＝1时，4n4＋1＝5为素数。

当n＞1时，2n2＋2n＋1＞2n2－2n＋1＞1，

所以4n4＋1只有在n＝1时才是素数的猜想是正确的。

后来法国女数学家索菲亚·惹曼(1776～1831)提出：形如n4＋4的数(n为自然数)，仅当n＝1时才是素数。

这也可用与欧拉完全类似的配方法证得。

证明:n4＋4＝(n2＋2)2－4n2

＝(n2＋2n＋2)(n2－2n＋2)

当n＝1时，n4＋4＝5是素数，

当n＞1时，n2＋2n＋2＞n2－2n＋2＞1，

所以，在n是自然数的情况下，仅当n＝1时，n4＋4才是素数。

最后，值得指出的是，经过科学家们的艰苦努力，已经找到一个产生素数的公式，它是

其中B＝m(n＋1)－(n!＋1)，(n!＝1·2·3·…·n)，m，n只能取素数值。

利用这个公式，任取一对素数m，n，可以求出一个素数，但是，公式在大多数情况下取值都是2。尽管如此，这个公式能产生全部素数，而且除了2以外，其他的素数恰好各取值一次。这是素数理论研究的一个重大突破。