数学领域：黄金分割数及其应用

0．618这个数叫黄金数，它与黄金分割有很大的关系。大约在两千多年前古希腊时期，数学家欧多克斯曾对此进行过研究。

什么叫黄金分割?将一线段分为两部分，使其满足条件：

全部：大部＝大部：小部

将线段如此分割，就叫做黄金分割(图(一))。

因为这种比在艺术和建筑上都很有用，中世纪意大利画家达·芬奇称它为黄金分割比。

设AB＝1，AP＝x，则PB＝1－x。由定义得

即x2＋x－1＝0

解此方程得x＝，舍去负值得

x＝＝0．618033988…≈0．618

它恰为我们刚刚提到的数值。

给定一条线段，如何用圆规直尺作出这一分割点P?

作法：1)过已知线段AB的端点B，作BC⊥AB，取BC＝AB；

2)连结AC，以C为圆心，CB为半径作圆弧交AC于D；

3)以A为圆心，AD为半径作圆弧交AB于P，则P为所求(图(二))。

证明：设AB＝a，则BC＝，根据勾股定理得

而

因此，P点分AB为黄金分割。

0．618有很多应用，但最重要的要算它在优选法中的应用。

优选法是尽可能少做试验、尽快地找到生产最优方案的方法，也就是现代科学实验的方法。华罗庚教授从60年代到70年代本着“洋为中用”宗旨把科学的方法普及到群众中去，收到了良好效果。(www.xing528.com)

使用优选法的步骤(先预备一张狭长纸条)：

1)请大家记好一个数字0．618。

2)举例说：进行某工艺时，温度的最佳点可能在1000℃～2000℃之间。当然，我们可以隔一度做一个试验，做完1000个试验之后，我们可以找到最佳温度，但要做1000次试验。

3)(取出纸条)假定这是有刻度的纸条，刻了1000℃到2000℃。第一个试验点在总长度的0．618处做，总长度是1000，乘以0．618是618，也就是说第一点在1618℃做，做出结果记下。

4)把纸条对折，在第一个试验点的对面，即点②(1382℃)处做第二个试验。

比较第一、二个试验点的结果，在较差点(例如①)处将纸条撕下不要。

5)对剩下的纸条，重复4)的处理方法，直到找出最好点。这种方法称为0．618法。

用这样的办法，普通工人一听就懂，懂了就用。华罗庚的这种讲授方法真是深入浅出的典型，是我们数学教育工作者学习的榜样。

关于0．618法的最优性，详细证明可参看1973年第2期《数学的实践与认识》杂志“论黄金分割的最优性”(洪加威)一文。这里只作直观说明。

为简单起见，设试验范围为[0，1](图(三))。

为比较试验结果，在[0，1]区间至少取两点c，c1。因为进行试验之前，预先并不知道这两点中哪个好，试验后，计算函数值后，可能去掉区间[0，c]或(c1，1]。因去掉它们的可能性是一样的，故有

c＝1－c1

此时c与c1点关于[0，1]的中点对称。

比较两点后，若去掉(c1，1]，留下[0，c1]，而c点在[0，c1]中的位置与c1在[0，1]中的相对位置一样，即它们的比应相等：

1∶c1＝c1∶c或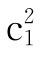＝c

把c＝1－c1；代入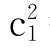＝c得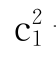＋c1－1＝0，解之得

因此，第一次试验应按c1＝0．618选点，无论去掉c1右边一段或c左边一段，留下范围的长度(c1或1－c)都是原定范围长度的0．618倍。

每做一次试验，范围就缩小为上次范围的0．618；n次试验后，范围就缩小成原来试验范围的(0．618)n。这样，经过少数几次试验可迅速找到较优的试验点，确定较优方案。