中国数学家的成果：等差级数的起源和应用

中国数学家很早就认识了等差级数，在中国最早的数学书《周髀算经》里谈到“七衡”(日月运行的圆周)的直径以19833里100步＋2递增，这就是等差级数。

约在公元1世纪成书的中国重要数学著作《九章算术》在《衰分》和《均输》二章里的问题和等差级数有关。

在5世纪末南北朝的张丘建在他著的《张丘建算经》就有三个问题是等差级数的问题：

[题一]今有女子善织布，逐日所织的布以仝数递增，已知第一日织五尺，经一月共织39丈，问逐日增多少?

答：5寸。

[题二]今有女子不善织布，逐日所织的布以仝数递减，已知第一日织五尺，末一日织一尺，计织30日。问共织布多少。

答：9丈。

[题三]今有某君以钱赠给许多人，先第一人给三钱，第二人给四钱，第三人给五钱，继续依次递增，钱给其他许多人。给完钱后把诸人所得的钱全部收回，再平均分派，结果每人得100钱，问人数多少?

答：195人。

唐朝和宋朝的数学家研究级数，并不是单纯追求趣味性，而是实际的需要。当时的天文学家都假定日、月、星辰在天空中的运动是等加速或等减速运动，每日经行的路程是等差级数。

比如唐朝的天文学家僧一行(683—727)，是世界上最早发现恒星在天上的位置会变动的天文学家。在他所著的《大衍历》里就是利用等差级数的求和公式来计算行星的行程。

宋朝时对等差级数和高阶等差级数的研究有最卓越的贡献的该是沈括(1031—1095)，他看到酒店、陶器店等把瓮、缸、瓦盆三类的东西推成长方台，底层排成一个长方形，以上的每层长阔各减少一个，因此他想要知道是否有简单的式子可以计算。

他看古算术书：《九章算术》的《商功》章原有长方台体积(古书称为“刍童”)的公式。用这公式来求实际的问题，常常是比原数少。因此他创造了新法《隙积法》以补“古书所不到者”。(“用刍童法求之，常失于数少，予思而得之。”)

假设长方台上底是a×b，下底是a′×b′共有n层，因为从上到下，每一层的纵横各增加一个，所以a′－a＝b′－b＝n－1，沈括的求和公式是：

ab＋(a＋1)(b＋1)＋(a＋2)(b＋2)＋…＋a′b′＝[(2a＋a′)b＋(2a′＋a)b′＋a′－a]×(www.xing528.com)

读者如果令a＝b＝1，a′＝b′＝n，代入以上的公式就可以得到

12＋22＋…＋n2＝n(n＋1)(2n＋1)/6

沈括留给后世的《梦溪笔谈》是一部内容丰富的科学著作，里面谈到数学、天文、物理、化学、生物、地质、地理、气象、医药和工程技术等，英国自然科学史家李约瑟教授对这书评价极高。而日本数学家三上义夫(Mikami Yoshio 1875—1950)对沈括非常推崇，他认为对古代数学来讲：“日本的数学家没有一个比得上沈括，像中根元圭精于医学、音乐和历书，但没有沈括的经世之才；本多利明精航海术，有经世才，但不能像沈括的多才多艺。如果在别国中能找到和沈括相比的数学家，那么德国的莱布尼兹和法国的卡罗，在某点上或可和沈括比较，但若一面远胜沈括，同时又多才多艺，那就谈不到了。仅有希腊的阿契泰斯，他的学识经验最能和沈括相比。总之沈括这样的人物，在全世界数学史上找不到，惟有中国出了这一个人。我把沈括当作中国数学家的模范人物或理想人物，是很恰当的。”(见《中国算学之特色》)

在沈括后，宋朝的数学家在级数研究有较好成果的，该算13世纪时的杨辉。他提出了三角垛公式：

1＋(1＋2)＋(1＋2＋3)＋…＋(1＋2＋3＋…＋n)＝n(n＋1)(n＋2)/6

左边的式子可以简写成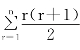，这样我们得到费马所发现的公式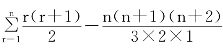，杨辉比他早三百多年就知道了这个事实。

元朝朱世杰是一个到处传授数学的教书先生，他在1299年写了一部《算学启蒙》以及1303年写的《四元玉鉴》就研究等差和高阶等差级数，特别是在后面那部著作，他扩充了杨辉的三角垛和公式，建立起属于

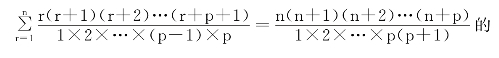公式，以及更复杂的公式。这些也是比费马早三百多年的时间。

朱世杰的书在17世纪流传到日本去，对日本数学家的级数理论的研究影响很大。反而在中国，自从朱世杰以后的400年来，级数理论却停顿着没有再发展。要到18世纪时的董祐诚和李善兰等才有一些论见。

级数理论和微积分学的产生有密切的关系，好像公式

＋n(n＋1)(2n＋1)/6，如果再加上一些极限概念家很早就有)，可以很容易算出球体的体积公式，中国数学家很早就用几何方法来推算球体的体积。在宋元的时候中国基本上具备了产生微积分的准备条件，可惜却没有一个人能像以后的西欧的莱布尼兹及牛顿那样承先启后的工作。更糟的是在明清时中国数学却衰退起来。

原因是在那里呢?最近中国数学工作者顾今用先生认为：“中国古代数学至少自秦汉有记载以来，许多方面一直居于世界上的遥遥领先的地位，发展到宋元之世，已经具备了西欧17世纪发明微积分前夕的许多条件，不妨说我们已经接近了微积分大门。尽管历代都有儒法斗争，儒家思想的阻挠放慢了数学发展的速度，甚至使许多创造湮没不彰或从此失传，但我们还是有可能先于欧洲发明微积分的。然而，宋朝的程朱理学已使当时的一些优秀数学家(例如杨辉)浪费精力于纵横图之类的数学游戏，陷入神秘主义，违反了我国自古以来的优良传统，到了明朝八股取士，理学统治了学术界的思想，我国的数学也就从此一落千丈了。”(见《数学学报》18卷第1期。

我想补充的一点是：欧洲那时期本上已完成封建社会过渡到资产阶级社会的阶段，生产力的提高自然提供了许多和生产有关系的如：热学、电磁学、流体力学等的问题产生在这种情形下，旧有的数学工具是不够解决这一类问题。一种崭新而能处理变动问题的有威力的新数学就要产生。而中国还是一个古老的封建社会，生产方式不改变，就束缚了它的科学发展。

看看过去，不必怪我们明清的老祖宗不争气，他们是有着社会条件的限制。“忆古伤怀易断肠”，还是“思今图强应加鞭”来得好。